题目内容
已知函数![]()
![]() ,在一周期内,当
,在一周期内,当![]() 时,
时,![]() 取得最大值3,当
取得最大值3,当![]() 时,
时,![]() 取得最小值-3,求
取得最小值-3,求
函数的解析式.
(2)求出函数![]() 的单调递增区间与对称轴方程,对称中心坐标;
的单调递增区间与对称轴方程,对称中心坐标;
(3)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(1)![]()
(2)![]() 对称中心坐标
对称中心坐标![]()
(3)![]()
解析:
(1)由题设知,A=3, ……………………1分
周期![]() =
=![]() ,
, ![]() ……………2分
……………2分
![]() ∴
∴![]() , ……………………3分
, ……………………3分
又∴![]() 时,
时,![]() 取得最大值3,即
取得最大值3,即![]() , …………5分
, …………5分
∴![]() . …………6分
. …………6分
(2) 由![]() 得
得![]()
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ………………8分
………………8分
由![]() 得:
得:![]()
对称轴方程为![]() ………10分
………10分
由![]() ,得
,得![]() ,
,
所以,该函数的对称中心为![]() . ---------------------12分
. ---------------------12分
(3)∵![]() ,∴
,∴![]() ………………… 14分
………………… 14分
由函数图像知
![]() , …………………………………16分
, …………………………………16分
注意:用“五点法”作出图象写答案参考得分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
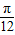 时,y取得最大值3,当x=
时,y取得最大值3,当x=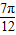 时,y取得最小值-3,
时,y取得最小值-3,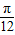 ,
,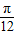 ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.