Question

已知函数f（x）=Asin（ωx+Φ）（A＞0，ω＞0，|x|＜π），在一周期内，当x=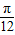时，y取得最大值3，当x=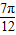时，y取得最小值-3，
求（1）函数的解析式．
（2）求出函数f（x）的单调递增区间与对称轴方程，对称中心坐标；
（3）当x∈[-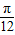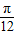，]时，求函数f（x）的值域．

Answer 1

【答案】分析：（1）由题干得出A，同一周期内两个最值点的横坐标之差的绝对值是半个T，从而得出ω，代入最高点坐标令ωx+Φ=求出φ，得函数的解析式；
（2）由（1）知：ω=2，φ=，把2x+看作X分别代入正弦函数的单调递增区间、对称轴方程、对称中心坐标分别求出x得函数f（x）的单调递增区间、对称轴方程、对称中心坐标；
（3）由x的范围得2x+的范围，由正弦函数的图象得sin（2x+）的范围，由不等式得3sin（2x+）的范围，即函数f（x）的值域．
解答：解：（1）由题设知，A=3，=-=，∴T=π，∴ω=2，
∴f（x）=3sin（2x+φ），∵3sin（2×+φ）=3，∴sin（+φ）=1，
∴+φ=，∴φ=，，∴f（x）=3sin（2x+）；
（2）由-+2kπ≤2x+≤+2kπ得-+kπ≤x≤+kπ，
∴函数f（x）的单调递增区间为[-+kπ，+kπ]（k∈Z），
由2x+=+kπ得x=+，
∴函数f（x）的对称轴方程为x=+（k∈Z），
由2x+=kπ得x=-+（k∈Z），
∴函数f（x）的对称中心坐标为（-+，0）（k∈Z）；
（3）∵x∈[-，]，∴2x+∈[，]，
∴sin（2x+）∈[，1]，∴3sin（2x+）∈[，3]，
∴函数f（x）的值域为[，3]．
点评：求y=Asin（ωx+φ）的解析式，条件不管以何种方式给出，一般先求A，再求ω，最后求φ；求y=Asin（ωx+φ）的单调递增区间、对称轴方程、对称中心坐标时，要把ωx+φ看作整体，分别代入正弦函数的单调递增区间、对称轴方程、对称中心坐标分别求出x，这儿利用整体的思想；求y=Asin（ωx+φ）的值域时，从x的范围由里向外扩，一直扩到
Asin（ωx+φ）的范围，即函数f（x）的值域．