题目内容
定义集合{x|a≤x≤b}的“长度”是b-a.已知m,n∈R,集合M={x|m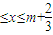 },N={x|n-
},N={x|n-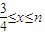 },且集合M,N都是集合{x|1≤x≤2}的子集,那么集合M∩N的“长度”的最小值是( )
},且集合M,N都是集合{x|1≤x≤2}的子集,那么集合M∩N的“长度”的最小值是( )A.

B.

C.
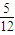
D.

【答案】分析:分别求出集合M,N的“长度”,当集合M,N表示的不等式在数轴上距离最远时,集合M∩N的“长度”最小,再求出此时的“长度”即可.
解答:解:∵集合M={x|m },
},
∴集合M的长度是 ,
,
∵集合N={x|n- },
},
∴集合的长度是 ,
,
∵M,N都是集合{x|1≤x≤2}的子集,
∴m最小为1,n最大为2,
此时集合M∩N的“长度”最小,为 .
.
故选C.
点评:本题主要考查了集合交集的运算,解题时要认真审题,仔细解答,注意新定义的判断.
解答:解:∵集合M={x|m
 },
},∴集合M的长度是
 ,
,∵集合N={x|n-
 },
},∴集合的长度是
 ,
,∵M,N都是集合{x|1≤x≤2}的子集,
∴m最小为1,n最大为2,
此时集合M∩N的“长度”最小,为
 .
.故选C.
点评:本题主要考查了集合交集的运算,解题时要认真审题,仔细解答,注意新定义的判断.

练习册系列答案
相关题目
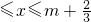 },N={x|n-
},N={x|n- },且集合M,N都是集合{x|1≤x≤2}的子集,那么集合M∩N的“长度”的最小值是
},且集合M,N都是集合{x|1≤x≤2}的子集,那么集合M∩N的“长度”的最小值是



 },N={x|n-
},N={x|n- },且集合M,N都是集合{x|1≤x≤2}的子集,那么集合M∩N的“长度”的最小值是( )
},且集合M,N都是集合{x|1≤x≤2}的子集,那么集合M∩N的“长度”的最小值是( )


