题目内容
已知椭圆的中心在原点,焦点在x轴上,一个顶点A(0,-1),且右焦点到右准线的距离为(1)求椭圆的方程.
(2)试问是否能找到一条斜率为k(k≠0)的直线l,使l与椭圆交于不同两点M、N且满足|AM|=|AN|?若这样的直线存在,求出k的取值范围;若不存在,请说明理由.
(1)解:设椭圆方程为![]() =1,由已知得b=1,
=1,由已知得b=1,![]() =
=![]() .
.
∴c=![]() ,a2=3.
,a2=3.
∴椭圆方程为![]() +y2=1.
+y2=1.
(2)解法一:设M(x1,y1)、N(x2,y2),MN中点P(x0,y0).
∴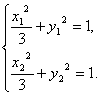 两式相减,得
两式相减,得
![]()
∴k=-![]() . ①
. ①
又∵|AM|=|AN|,
∴AP⊥MN.
∴kAP=-![]() ,即
,即![]() =-
=-![]() . ②
. ②
联立①②,解得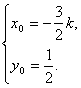
若直线l存在,则P在椭圆内部.
∴![]() +y02<1,从而得k2<1.
+y02<1,从而得k2<1.
∴-1<k<1且k≠0.
∴满足条件的直线l存在,且k∈(-1,0)∪(0,1).
解法二:设直线l的方程为y=kx+m,代入椭圆![]() +y2=1且整理得(1+3k2)x2+6kmx+3(m2-1)=0.
+y2=1且整理得(1+3k2)x2+6kmx+3(m2-1)=0.
要使l与椭圆相交于不同两点,
∴Δ>0,即(6km)2-4(1+3k2)×3(m2-1)>0.化简得3k2-m2+1>0. (*)
又∵|AM|=|AN|,P为MN的中点,
∴MN⊥AP.
∴k·kAP=-1.
而x0=![]() =-
=-![]() ,
,
y0=![]() ,
,
∴kAP=-![]() .
.
∴2m=1+3k2,即m=![]() .
.
代入不等式(*)可得k2<1.
∴-1<k<1且k≠0.

练习册系列答案
相关题目