题目内容
(本小题满分12分)已知椭圆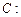
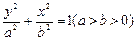 经过点
经过点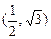 ,一个焦点是
,一个焦点是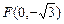 .
.
(Ⅰ)求椭圆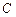 的方程;
的方程;
(Ⅱ)设椭圆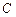 与
与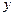 轴的两个交点为
轴的两个交点为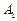 、
、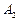 ,点
,点 在直线
在直线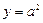 上,直线
上,直线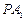 、
、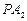 分别与椭圆
分别与椭圆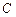 交于
交于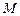 、
、 两点.试问:当点
两点.试问:当点 在直线
在直线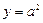 上运动时,直线
上运动时,直线 是否恒经过定点
是否恒经过定点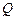 ?证明你的结论.
?证明你的结论.
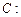
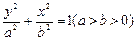 经过点
经过点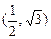 ,一个焦点是
,一个焦点是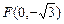 .
.(Ⅰ)求椭圆
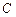 的方程;
的方程;(Ⅱ)设椭圆
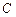 与
与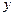 轴的两个交点为
轴的两个交点为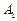 、
、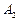 ,点
,点 在直线
在直线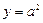 上,直线
上,直线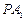 、
、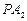 分别与椭圆
分别与椭圆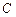 交于
交于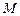 、
、 两点.试问:当点
两点.试问:当点 在直线
在直线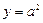 上运动时,直线
上运动时,直线 是否恒经过定点
是否恒经过定点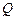 ?证明你的结论.
?证明你的结论.(本小题满分12分)
解:(I)方法1:椭圆的一个焦点是 ,
,
∴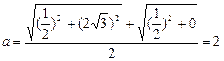 , ………………(2分)
, ………………(2分)
∵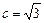 ,∴
,∴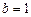 ,∴椭圆方程为
,∴椭圆方程为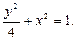 ………………(4分)
………………(4分)
方法2: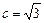 ,可设椭圆方程为
,可设椭圆方程为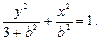 ………………(2分)
………………(2分)
∵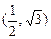 在椭圆上,所以
在椭圆上,所以 (舍去)
(舍去)
∴椭圆方程为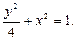 ………………(4分)
………………(4分)
(II)
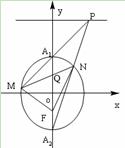
方法1:当点 在
在 轴上时,
轴上时, 、
、 分别与
分别与 、
、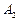 重合,
重合,
若直线 通过定点
通过定点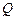 ,则
,则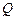 必在
必在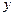 轴上,设
轴上,设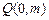 ,………………(6分)
,………………(6分)
当点 不在
不在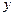 轴上时,设
轴上时,设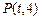 ,
,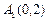 、
、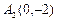 ,
,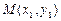 ,
,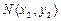
直线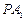 方程
方程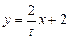 ,
,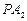 方程
方程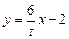 ,
,
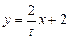 代入
代入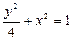 得
得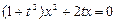 ,
,
解得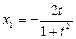 ,
, ,
,
∴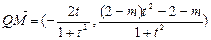 , ……………(8分)
, ……………(8分)
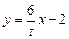 代入
代入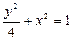 得
得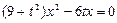
解得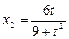 ,
,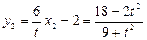 ,
,
∴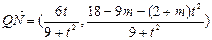 , ………………(10分)
, ………………(10分)
∵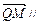
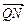 ,
,
∴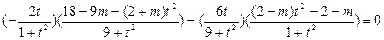 ,
,
∴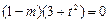 ,
,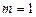 ,
,
∴当点 在直线
在直线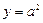 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点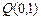 .……………(12分)
.……………(12分)
方法2:直线 恒经过定点
恒经过定点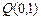 ,证明如下:
,证明如下:
当 斜率不存在时,直线
斜率不存在时,直线 即
即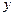 轴,通过点
轴,通过点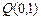 ,……………(6分)
,……………(6分)
当点 不在
不在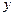 轴上时,设
轴上时,设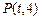 ,
,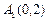 、
、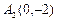 ,
,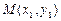 ,
,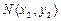
直线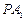 方程
方程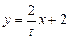 ,
,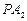 方程
方程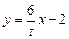 ,
,
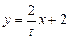 代入
代入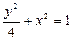 得
得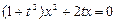 ,
,
得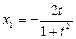 ,
, ,∴
,∴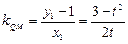 ,……………(8分)
,……………(8分)
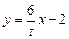 代入
代入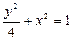 得
得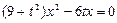
得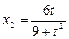 ,
,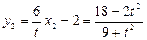 ,
,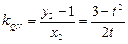 …………(10分)
…………(10分)
∴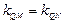 ,直线
,直线 恒经过定点
恒经过定点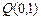 . ………………(12分)
. ………………(12分)
方法3:∵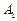 、
、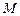 、
、 三点共线,
三点共线,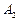 、
、 、
、 三点也共线,
三点也共线,
∴ 是直线
是直线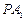 与直线
与直线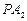 的交点,
的交点,
当 斜率存在时,设
斜率存在时,设 :
: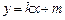 ,代入
,代入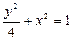 ,
,
得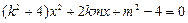 ,
,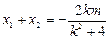 ,
,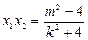 ,
,
直线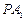 方程
方程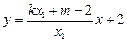 ,直线
,直线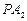 方程
方程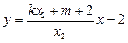 ,
,
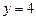 分别代入,得
分别代入,得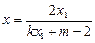 ,
, ,
,
∴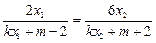 ,即
,即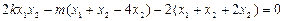 ,
,
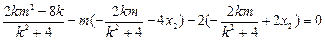 ,
,
∴ 对任意变化的
对任意变化的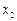 都成立,只能
都成立,只能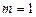 ,
,
∴直线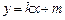 ,通过点
,通过点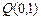
当 斜率不存在时,直线
斜率不存在时,直线 即
即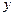 轴,通过点
轴,通过点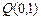 ,……………(10分)
,……………(10分)
∴当点 在直线
在直线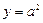 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点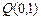 .
.
解:(I)方法1:椭圆的一个焦点是
 ,
,∴
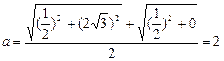 , ………………(2分)
, ………………(2分)∵
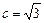 ,∴
,∴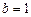 ,∴椭圆方程为
,∴椭圆方程为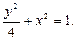 ………………(4分)
………………(4分)方法2:
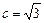 ,可设椭圆方程为
,可设椭圆方程为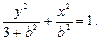 ………………(2分)
………………(2分)∵
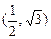 在椭圆上,所以
在椭圆上,所以 (舍去)
(舍去)∴椭圆方程为
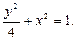 ………………(4分)
………………(4分)(II)

方法1:当点
 在
在 轴上时,
轴上时, 、
、 分别与
分别与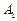 、
、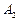 重合,
重合,若直线
 通过定点
通过定点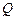 ,则
,则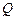 必在
必在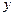 轴上,设
轴上,设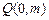 ,………………(6分)
,………………(6分)当点
 不在
不在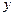 轴上时,设
轴上时,设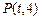 ,
,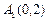 、
、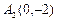 ,
,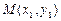 ,
,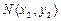
直线
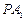 方程
方程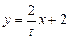 ,
,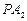 方程
方程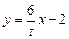 ,
,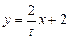 代入
代入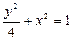 得
得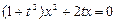 ,
,解得
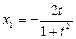 ,
, ,
,∴
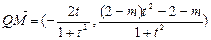 , ……………(8分)
, ……………(8分)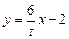 代入
代入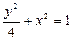 得
得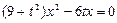
解得
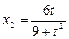 ,
,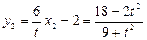 ,
,∴
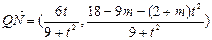 , ………………(10分)
, ………………(10分)∵
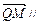
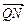 ,
,∴
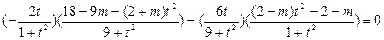 ,
,∴
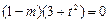 ,
,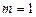 ,
,∴当点
 在直线
在直线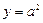 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点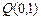 .……………(12分)
.……………(12分)方法2:直线
 恒经过定点
恒经过定点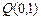 ,证明如下:
,证明如下:当
 斜率不存在时,直线
斜率不存在时,直线 即
即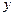 轴,通过点
轴,通过点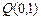 ,……………(6分)
,……………(6分)当点
 不在
不在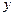 轴上时,设
轴上时,设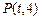 ,
,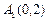 、
、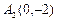 ,
,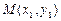 ,
,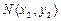
直线
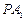 方程
方程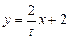 ,
,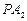 方程
方程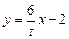 ,
,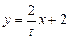 代入
代入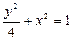 得
得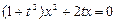 ,
,得
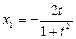 ,
, ,∴
,∴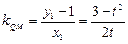 ,……………(8分)
,……………(8分)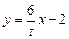 代入
代入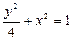 得
得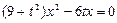
得
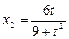 ,
,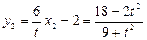 ,
,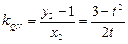 …………(10分)
…………(10分)∴
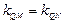 ,直线
,直线 恒经过定点
恒经过定点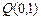 . ………………(12分)
. ………………(12分)方法3:∵
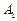 、
、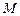 、
、 三点共线,
三点共线,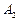 、
、 、
、 三点也共线,
三点也共线,∴
 是直线
是直线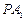 与直线
与直线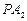 的交点,
的交点,当
 斜率存在时,设
斜率存在时,设 :
: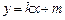 ,代入
,代入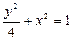 ,
,得
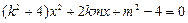 ,
,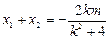 ,
,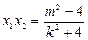 ,
,直线
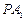 方程
方程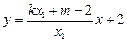 ,直线
,直线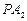 方程
方程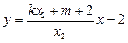 ,
,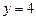 分别代入,得
分别代入,得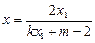 ,
, ,
,∴
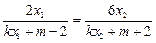 ,即
,即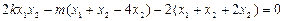 ,
,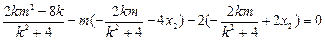 ,
,∴
 对任意变化的
对任意变化的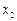 都成立,只能
都成立,只能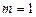 ,
,∴直线
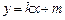 ,通过点
,通过点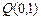
当
 斜率不存在时,直线
斜率不存在时,直线 即
即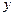 轴,通过点
轴,通过点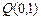 ,……………(10分)
,……………(10分)∴当点
 在直线
在直线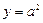 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点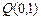 .
.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为坐标原点,
为坐标原点,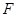 为椭圆
为椭圆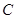 :
: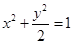 在
在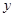 轴正半轴上的焦点,过
轴正半轴上的焦点,过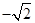 的直线
的直线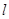 与
与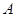 、
、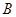 两点,点
两点,点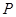 满足
满足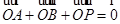 .
.
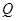 ,证明:
,证明: (
( )的一个焦点坐标为
)的一个焦点坐标为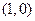 ,且长轴长是短轴长的
,且长轴长是短轴长的 倍.
倍.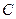 的方程;
的方程;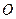 为坐标原点,椭圆
为坐标原点,椭圆 相交于两个不同的点
相交于两个不同的点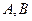 ,线段
,线段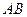 的中点为
的中点为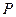 ,若直线
,若直线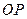 的斜率为
的斜率为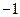 ,求△
,求△ 的面积.
的面积. 的焦点为顶点,顶点为焦点的椭圆方程为
的焦点为顶点,顶点为焦点的椭圆方程为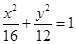
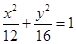

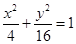
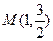 ,两个焦点为
,两个焦点为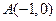 ,
,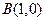 ,O为坐标原点。
,O为坐标原点。 过点
过点 ,且离心率为
,且离心率为 .
. 的方程;
的方程; 为椭圆
为椭圆 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 分别交直线
分别交直线 于
于 两点.证明:当点
两点.证明:当点 恒为定值.
恒为定值.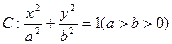 经过点(p,q),离心率
经过点(p,q),离心率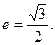 其中p,q分别表示标准正态分布的期望值与标准差。
其中p,q分别表示标准正态分布的期望值与标准差。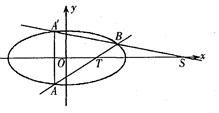
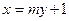 与椭圆C交于A,B两点,点A关于x轴的对称点为
与椭圆C交于A,B两点,点A关于x轴的对称点为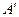
 。①试建立
。①试建立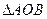 的面积关于m的函数关系;②莆田十中高三(1)班数学兴趣小组通过试验操作初步推断:“当m变化时,直线
的面积关于m的函数关系;②莆田十中高三(1)班数学兴趣小组通过试验操作初步推断:“当m变化时,直线 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。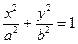 的左右焦点分别为
的左右焦点分别为 ,P为椭圆上一点,且
,P为椭圆上一点,且 ,则椭圆的离心率e=__________。
,则椭圆的离心率e=__________。 圆心为A;动圆M过点
圆心为A;动圆M过点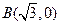 且与圆A相切,圆心M 的坐标为
且与圆A相切,圆心M 的坐标为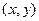 且
且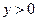 ,它的轨迹记为
,它的轨迹记为 C。
C。 C的方程;
C的方程;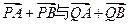 互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。
互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。