题目内容
9.设f(1)=2,f(n)>0(n∈N+),且f(n1+n2)=f(n1)f(n2)(1)求f(2),f(3),f(4);
(2)猜想f(n)的解析式;
(3)证明你的猜想.
分析 (1)直接利用已知条件求出f(2)、f(3)、f(4)的值;
(2)利用(1)猜想f(n)的解析式;
(3)然后利用数学归纳法的证明方法证明即可
解答 解:(1)f(1)=2,f(n1+n2)=f(n1)•f(n2)
∴f(2)=f(1+1)=f(1)•f(1)=22=4;
f(3)=f(2+1)=f(2)•f(1)=22•2=8;
f(4)=f(3+1)=f(3)•f(1)=23•2=16;
(2)猜想f(n)=2n,n∈N*
(3)用数学归纳法证明如下:
①当n=1时,f(1)=21=2,∴猜想正确;
②假设当n=k(k≥1)时猜想正确,即f(k)=2k,k∈N*
那么当n=k+1时,f(k+1)=f(k)f(1)=2k•2=2k+1
所以,当n=k+1时,猜想正确
由①②知,对n∈N*,f(n)=2n,正确.
点评 本题考查数学归纳法的证明方法的应用,考查逻辑推理能力以及计算能力.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
14.使平面α∥平面β的一个条件是( )
| A. | 存在一条直线a,a∥α,a∥β | |
| B. | 存在一条直线a,a?α,a∥β | |
| C. | 存在两条平行直线a、b,a?α,b?β,a∥β,b∥α | |
| D. | 存在两条异面直线a、b,a?α,b?β,a∥β,b∥α |
1.已知集合M={x|(1-x)x>0},N={y|y=x2+2x+3},则(∁RM)∩N=( )
| A. | {x|0<x<1} | B. | {x|x>1} | C. | {x|x≥2} | D. | {x|1<x<2} |
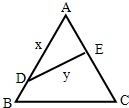 如图,某公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,某公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上. 如图是教材选修1-2中《推理与证明》一章的知识结构图,请把A处填入适当的方法综合法.
如图是教材选修1-2中《推理与证明》一章的知识结构图,请把A处填入适当的方法综合法.