题目内容
14．使平面α∥平面β的一个条件是（ ）| A． | 存在一条直线a，a∥α，a∥β | |
| B． | 存在一条直线a，a?α，a∥β | |
| C． | 存在两条平行直线a、b，a?α，b?β，a∥β，b∥α | |
| D． | 存在两条异面直线a、b，a?α，b?β，a∥β，b∥α |
分析 依据面面平行的定义与定理依次判断排除错误的，筛选出正确的即可得解．
解答 解：对于A，一条直线与两个平面都平行，两个平面不一定平行．故A不对；
对于B，一个平面中的一条直线平行于另一个平面，两个平面不一定平行，故B不对；
对于C，两个平面中的两条直线平行，不能保证两个平面平行，故C不对；
对于D，两个平面中的两条互相异面的直线分别平行于另一个平面，可以保证两个平面平行，故D正确．
故选：D．
点评 考查面面平行的判定定理，依据条件由定理直接判断，属于中档题．
练习册系列答案
相关题目
2．两条异面直线在同一平面内的射影不可能是（ ）
| A． | 两条相交直线 | |
| B． | 两条平行直线 | |
| C． | 一条直线和不在这条直线上的一个点 | |
| D． | 两个点 |
19．（理）在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，则异面直线AC1与B1C所成角的余弦值为（ ）
| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{{2\sqrt{2}}}{5}$ | D． | $-\frac{{2\sqrt{2}}}{5}$ |
6．已知复数Z=$\frac{1-\sqrt{3}i}{\sqrt{3}+i}$，$\overline{Z}$是Z的共轭复数，则Z•$\overline{Z}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | 4 | D． | 1 |
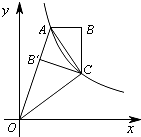如图，双曲线y=$\frac{2}{x}$（x＞0）经过四边形OABC的顶点A、C，∠ABC=90°，OC平分OA与x轴正半轴的夹角，AB∥x轴，将△ABC沿AC翻折后得△AB′C，B′点落在OA上，则四边形OABC的面积是2．