题目内容
在△ABC中,满足tan| A-B |
| 2 |
| a-b |
| a+b |
(1)试判断△ABC的形状;
(2)当a=10,c=10时,求tan
| A |
| 2 |
分析:(1)根据题设,可推断当a=b和a≠b两种情况.当a=b可推断△ABC为等腰三角形;当a≠b时通过正弦定理及题设,求得cot
的值,进而求出A+B进而推断△ABC的形状.
(2)根据a=c排除△ABC为直角三角形的情况,根据(1)可知a=b,进而推断△ABC为等边三角形,进而求出∠A和tan
的值.
| A+B |
| 2 |
(2)根据a=c排除△ABC为直角三角形的情况,根据(1)可知a=b,进而推断△ABC为等边三角形,进而求出∠A和tan
| A |
| 2 |
解答:解:(1)∵tan
=
当a=b时,△ABC为等腰三角形
当a≠b时,根据正弦定理
=
=
=tan
∴cot
=1,即
=
,A+B=
∴△ABC为以C为直角的直角三角形.
∴△ABC为直角三角形或等腰三角形
(2)a=c=10,排除△ABC为直角三角形,则△ABC为等腰三角形,即a=b,
又a=c=10,所以a=c=b
∠A=60°
故tan
=tan30°=
| A-B |
| 2 |
| a-b |
| a+b |
当a=b时,△ABC为等腰三角形
当a≠b时,根据正弦定理
| a-b |
| a+b |
| sinA-sinB |
| sinA+sinB |
2cos(
| ||||
2sin(
|
| A-B |
| 2 |
∴cot
| A+B |
| 2 |
| A+B |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴△ABC为以C为直角的直角三角形.
∴△ABC为直角三角形或等腰三角形
(2)a=c=10,排除△ABC为直角三角形,则△ABC为等腰三角形,即a=b,
又a=c=10,所以a=c=b
∠A=60°
故tan
| A |
| 2 |
| ||
| 3 |
点评:本题主要考查和差化积和同角三角函数的基本关系的应用.属基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 如图,在△ABC中,AD⊥BC,
如图,在△ABC中,AD⊥BC,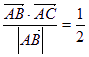 ,
,  , 又点E在BC边上, 且满足
, 又点E在BC边上, 且满足 ),为奇函数,则a=1;
),为奇函数,则a=1; ,其中θ∈(π,
,其中θ∈(π, ),则
),则
 =a,
=a, =b,若a•b<0,则△ABC是钝角三角形
=b,若a•b<0,则△ABC是钝角三角形 ,λ∈(0,+∞),则直线AP一定通过△ABC的内心.
,λ∈(0,+∞),则直线AP一定通过△ABC的内心.