题目内容
设x=4是函数f(x)=(x2+ax+b)e4-x(x∈R)的一个极值点;(I)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(Ⅱ)设a>0,g(x)=
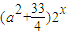 ,若存在ξ1,ξ2∈[0,5]使得|f(ξ1)-g(ξ2)|<4成立,求a的取值范围.
,若存在ξ1,ξ2∈[0,5]使得|f(ξ1)-g(ξ2)|<4成立,求a的取值范围.
【答案】分析:(I)由题意可得f′(4)=0,即可用a表示b,通过对a分类讨论,解出f′(x)>0,f′(x)<0即可;
(II)利用(I)的结论即可得出函数f(x)的值域,利用函数g(x)的单调性即可得出值域,可得值域的交集=[m,n].由存在ξ1,ξ2∈[0,5]使得|f(ξ1)-g(ξ2)|<4成立?|m-n|<4,解出即可.
解答:解:(I)∵f'(x)=(2x+a-x2-ax-b)e4-x=-[x2+(a-2)x+b-a]e4-x
由f'(4)=0,得16+(a-2)4+b-a=0
即b=-3a-8,
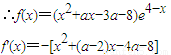
=-(x-4)(x+a+2)e4-x

在[-a-2,+∞)上为减函数.

在[4,+∞)上为减函数.
(II)当a>0时,-a-2<0,
∴f(x)在[0,4]上为增函数,在[4,5]上为减函数,
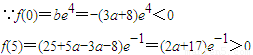
∴f(0)<f(5),
f(4)=16+4a-3a-8=a+8,

∴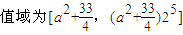 ,
,
∵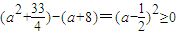 ,
,
若存在ξ1,ξ2∈[0,5]使得|f(ξ1)-g(ξ2)|<4成立.
只要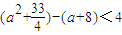 ,
,
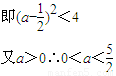
故 .
.
点评:熟练掌握利用导数研究函数的单调性、极值与最值、等价转化等是解题的关键.
(II)利用(I)的结论即可得出函数f(x)的值域,利用函数g(x)的单调性即可得出值域,可得值域的交集=[m,n].由存在ξ1,ξ2∈[0,5]使得|f(ξ1)-g(ξ2)|<4成立?|m-n|<4,解出即可.
解答:解:(I)∵f'(x)=(2x+a-x2-ax-b)e4-x=-[x2+(a-2)x+b-a]e4-x
由f'(4)=0,得16+(a-2)4+b-a=0
即b=-3a-8,
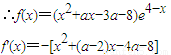
=-(x-4)(x+a+2)e4-x

在[-a-2,+∞)上为减函数.

在[4,+∞)上为减函数.
(II)当a>0时,-a-2<0,
∴f(x)在[0,4]上为增函数,在[4,5]上为减函数,
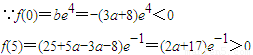
∴f(0)<f(5),
f(4)=16+4a-3a-8=a+8,

∴
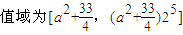 ,
,∵
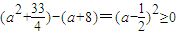 ,
,若存在ξ1,ξ2∈[0,5]使得|f(ξ1)-g(ξ2)|<4成立.
只要
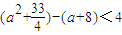 ,
,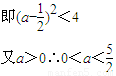
故
 .
.点评:熟练掌握利用导数研究函数的单调性、极值与最值、等价转化等是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目