题目内容
定义在[-6,6]上的偶函数f(x)在区间[0,6]上是减函数,且f(3)=0,则不等式xf(x)>0的解集是( )
分析:利用函数f(x)是偶函数,且f(3)=0,得到f(-3)=0,然后利用函数f(x)在区间[0,6]上是减函数,得到函数在[-6,0]上为增函数,从而得到函数f(x)的取值,解不等式即可.
解答:解:∵函数f(x)是定义在[-6,6]上的偶函数,在区间[0,6]上是减函数,且f(3)=0
∴函数在[-6,0]上为增函数,且f(-3)=-f(3)=0,(如图,直线只代表函数的单调性.)
∴当-3<x<3时,f(x)>0,
当3<x≤6或-6≤x<-3时,f(x)<0.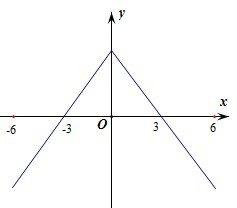
当x>0时,不等式xf(x)>0,等价为f(x)>0.此时0<x<3.
当x<0时,不等式xf(x)>0,等价为f(x)<0.此时-6≤x<-3.
∴不等式xf(x)>0的解集为 {x|-6≤x<-3或0<x<3}.
故选C.
∴函数在[-6,0]上为增函数,且f(-3)=-f(3)=0,(如图,直线只代表函数的单调性.)
∴当-3<x<3时,f(x)>0,
当3<x≤6或-6≤x<-3时,f(x)<0.

当x>0时,不等式xf(x)>0,等价为f(x)>0.此时0<x<3.
当x<0时,不等式xf(x)>0,等价为f(x)<0.此时-6≤x<-3.
∴不等式xf(x)>0的解集为 {x|-6≤x<-3或0<x<3}.
故选C.
点评:本题主要考查函数奇偶性和单调性的应用,利用数形结合是解决此类问题的关键.

练习册系列答案
相关题目
f(x)是定义在[-6,6]上的偶函数,且f(-3)>f(1),则下列各式一定成立的是( )
| A、f(0)<f(6) | B、f(3)>f(2) | C、f(-1)<f(3) | D、f(2)>f(0) |