题目内容
11.解方程:|2x+3|-|x-1|=4x-3.分析 把要解的方程去掉绝对值,化为与之等价的3个式子,求得每个式子的解,从而得出结论.
解答 解:|2x+3|-|x-1|=4x-3,即 $\left\{\begin{array}{l}{x<-\frac{3}{2}}\\{-2x-3-(1-x)=4x-3}\end{array}\right.$①,或$\left\{\begin{array}{l}{-\frac{3}{2}≤x<1}\\{2x+3-(1-x)=4x-3}\end{array}\right.$ ②,
或 $\left\{\begin{array}{l}{x≥1}\\{2x+3-(x-1)=4x-3}\end{array}\right.$③.
解①求得x无解,解②求得x无解,解③求得x=$\frac{7}{3}$.
综上可得,x=$\frac{7}{3}$.
点评 本题主要考查带有绝对值的方程的求法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
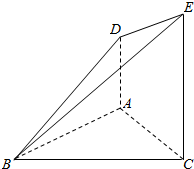 如图所示,AD⊥平面ABC,CE⊥平面ABC,CE=2AD,AC=AB=1,BC=$\sqrt{2}$,证明:
如图所示,AD⊥平面ABC,CE⊥平面ABC,CE=2AD,AC=AB=1,BC=$\sqrt{2}$,证明: 如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.
如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.
 如图,在三棱锥A-BCD中,AB=BC=CD=DA=AC,BD=$\sqrt{2}$AB,求证:平面ABD⊥平面BCD.
如图,在三棱锥A-BCD中,AB=BC=CD=DA=AC,BD=$\sqrt{2}$AB,求证:平面ABD⊥平面BCD.