题目内容
1. 如图,在三棱锥A-BCD中,AB=BC=CD=DA=AC,BD=$\sqrt{2}$AB,求证:平面ABD⊥平面BCD.
如图,在三棱锥A-BCD中,AB=BC=CD=DA=AC,BD=$\sqrt{2}$AB,求证:平面ABD⊥平面BCD.
分析 取BD的中点O,连接OA,OC,证明AO⊥OC,AO⊥BD,OC∩BD=O,可得AO⊥平面BCD,即可证明平面ABD⊥平面BCD.
解答 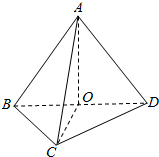 证明:取BD的中点O,连接OA,OC,
证明:取BD的中点O,连接OA,OC,
∵AB=BC=CD=DA,
∴AO⊥BD,CO⊥BD,
∵BD=$\sqrt{2}$AB,
∴AO=CO=$\frac{\sqrt{2}}{2}$AB,
∴AO2+CO2=AC2,
∴AO⊥OC,
∵AO⊥BD,OC∩BD=O,
∴AO⊥平面BCD,
∵AO?平面ABD,
∴平面ABD⊥平面BCD.
点评 本题考查线面、面面垂直的判定,考查学生分析解决问题的能力,证明AO⊥平面BCD是关键.

练习册系列答案
相关题目
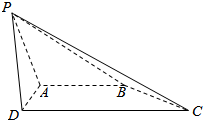 如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD.AD⊥CD,CD=2AB=2AD=4,侧面PAD为正三角形,AB⊥PA.
如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD.AD⊥CD,CD=2AB=2AD=4,侧面PAD为正三角形,AB⊥PA.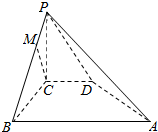 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证:
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证: 如图所示,已知三棱锥O-ABC的三条侧棱OA、OB、OC两两垂直,△ABC为等边三角形,M为△ABC内部一点,点P在OM的延长线上,且PA=PB.
如图所示,已知三棱锥O-ABC的三条侧棱OA、OB、OC两两垂直,△ABC为等边三角形,M为△ABC内部一点,点P在OM的延长线上,且PA=PB.