题目内容
已知函数 .
.
(1)当 时,画出函数
时,画出函数 的简图,并指出
的简图,并指出 的单调递减区间;
的单调递减区间;
(2)若函数 有4个零点,求a的取值范围.
有4个零点,求a的取值范围.
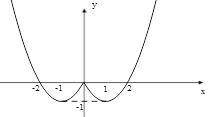
(1)函数 的简图如下图所示,
的简图如下图所示, 的单调递减区间为
的单调递减区间为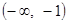 和
和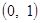 ;
;
(2)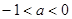 .
.
解析试题分析: (1)将 代入解析式,然后去掉绝对值,得一个两段都为二次函数的分段函数:
代入解析式,然后去掉绝对值,得一个两段都为二次函数的分段函数: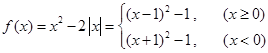 ,据此可画出图象,由图象可得
,据此可画出图象,由图象可得 的单调递减区间.
的单调递减区间.
(2)由 ,得
,得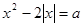 ,这样问题转化为曲线
,这样问题转化为曲线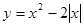 与直线
与直线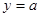 有4个不同交点,由(1)题中的图像可得a的取值范围.
有4个不同交点,由(1)题中的图像可得a的取值范围.
试题解析:(1)当 时,
时,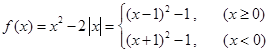 ,
,
由图可知, 的单调递减区间为
的单调递减区间为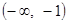 和
和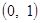 . 6分
. 6分
(2)由 ,得
,得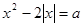 ,
,
∴曲线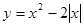 与直线
与直线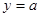 有4个不同交点,
有4个不同交点,
∴根据(1)中图像得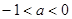 . 12分
. 12分
考点:1、函数的图象;2、函数的单调区间;3、函数的零点.

练习册系列答案
相关题目
 与时刻x的关系为
与时刻x的关系为 ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且 ,若用每天
,若用每天 .
. ,求t的取值范围;
,求t的取值范围; 的图象分别与
的图象分别与 轴、
轴、 轴交于
轴交于 两点,且
两点,且 ,函数
,函数 ,当
,当 ,时,求函数
,时,求函数 的值域.
的值域. 是定义在
是定义在 上的增函数,且
上的增函数,且
 的值;(2)、若
的值;(2)、若 ,解不等式
,解不等式 .
. 的一部分,栏栅与矩形区域的边界交于点
的一部分,栏栅与矩形区域的边界交于点 ,交曲线于点
,交曲线于点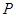 ,设
,设 .
.
 (
( 为坐标原点)的面积
为坐标原点)的面积 表示成
表示成 的函数
的函数 ;
; 处,
处, 的值及
的值及 (a,b均为正常数).
(a,b均为正常数).  在
在 内至少有一个零点;
内至少有一个零点; 处有极值,
处有极值, ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围; 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围.
的取值范围. :
: 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围; ,当
,当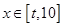 时,
时, 的值域为区间
的值域为区间 ,且
,且 .
.
 的值,据此提出一个猜想,并予以证明;
的值,据此提出一个猜想,并予以证明; 的下方.
的下方. .
. 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程; 时,讨论函数
时,讨论函数 在区间
在区间 上的单调性;
上的单调性; 对任意
对任意 成立.
成立.