题目内容
已知函数
（1）计算
的值，据此提出一个猜想，并予以证明；
（2）证明：除点（2,2）外，函数的图像均在直线
的下方.
（1）
，
，猜想详见解析；（2）证明过程详见解析.
解析试题分析：本题考查求函数值和函数最值、函数的对称性等基础知识，考查学生的转化能力、分析问题解决问题的能力和计算能力.第一问，直接代入
求函数值，通过2组数的规律得到猜想，利用对称关系证明结论；第二问，先求出函数的定义域，利用单调性的定义判断函数的单调性，求最值，将原结论转化为求最值问题.
试题解析： （1）∵
∴；
猜想：
的图象关于
对称，下面证明猜想的正确性；
∵
∴的图象关于对称
（2）∵的定义域为
，由（1）知的图象关于对称
设
∴
∵
∴
又
∴
∴为
上的增函数，由对称性知在
上为减函数，
∴
∴
的图象除点
外均在直线的下方.
考点：1.证明函数的对称性；2.函数单调性的定义.
练习册系列答案
相关题目
对任意实数
均有
，且当
时
；
时， 对
恒有
，求实数
的取值范围.
.
时，画出函数
的简图，并指出
，
时，判断并证明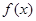
的奇偶性；
，使得
的定义域为 
，值域为
，则称函数
是
上的“四维方军”函数，求常数
的值；
使函数
是区间
的值，否则，请说明理由．
.
在其定义域内为单调递增函数，求实数
的取值范围；
，且
，若在
上至少存在一点
，使得
成立，求实数
在区间
上的最大值、最小值分别是
，集合
．
，且
，求
，且
，记
，求
的最小值．
对一切
R恒成立，求实数
的取值范围；
是定义在
上的奇函数，当
时，
，求
-2alnx（a>0）