题目内容
已知函数 的图象分别与
的图象分别与 轴、
轴、 轴交于
轴交于 两点,且
两点,且 ,函数
,函数 ,当
,当 满足不等式
满足不等式 ,时,求函数
,时,求函数 的值域.
的值域.
 .
.
解析试题分析:求函数 的值域,首先求函数的解析式,因为函数
的值域,首先求函数的解析式,因为函数 ,函数
,函数 ,只需求出
,只需求出 的值即可,由已知函数
的值即可,由已知函数 的图象分别与
的图象分别与 轴、
轴、 轴交于
轴交于 两点,可求出
两点,可求出 的坐标(用
的坐标(用 表示),从而写出
表示),从而写出 的坐标,再由已知
的坐标,再由已知 ,利用复数相等的定义,可求出
,利用复数相等的定义,可求出 的值,可得
的值,可得 的解析式,又
的解析式,又 ,可得
,可得 ,由基本不等式及单调性,从而得值域.
,由基本不等式及单调性,从而得值域.
试题解析:  ,又
,又 ,所以K=2,又
,所以K=2,又 ,可得
,可得 ,
, =
= 因为
因为 ,所以函数值域为
,所以函数值域为
考点:求函数解析式,解一元二次不等式,基本不等式.

练习册系列答案
相关题目
 ,两个函数
,两个函数 ,
,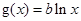 的图像关于直线
的图像关于直线 对称.
对称. 满足的关系式;
满足的关系式; 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点; 时,在
时,在 上解不等式
上解不等式 .
. ,
, 是定义域为
是定义域为 的奇函数.
的奇函数. 的值,判断并证明当
的值,判断并证明当 时,函数
时,函数 ,函数
,函数 ,求
,求 的值域;
的值域; ,若
,若 对于
对于 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数 .
. 对任意实数
对任意实数 均有
均有 ,且当
,且当 时
时
 ;
; 时, 对
时, 对 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围. ,
, 上的奇函数
上的奇函数
 值;(4分)
值;(4分) 在
在 上单调递增,且
上单调递增,且 ,求实数
,求实数 的取值范围.(6分)
的取值范围.(6分) 是定义域为R的奇函数,
是定义域为R的奇函数, ,
, 的值;
的值; 在x∈[2,3]上恒成立,求
在x∈[2,3]上恒成立,求 的取值范围.
的取值范围. .
. 时,画出函数
时,画出函数 的简图,并指出
的简图,并指出 在区间
在区间 上的最大值、最小值分别是
上的最大值、最小值分别是 ,集合
,集合 .
. ,且
,且 ,求
,求 ,且
,且 ,记
,记 ,求
,求 的最小值.
的最小值.