题目内容
(本题13分)
已知平面直角坐标系内三点
(1) 求过 三点的圆的方程,并指出圆心坐标与圆的半径.
三点的圆的方程,并指出圆心坐标与圆的半径.
(2)求过点 与条件 (1) 的圆相切的直线方程.
与条件 (1) 的圆相切的直线方程.
(1) 圆的方程为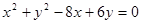 ,圆心是
,圆心是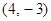 、半径
、半径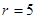
(2)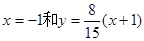
解析试题分析:(1)设圆的方程为: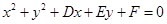 ,
,
将三个带你的坐标分别代入圆的方程,解得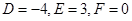 ,
,
所以圆的方程为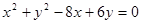 ,圆心是
,圆心是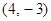 、半径
、半径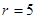 . ……7分
. ……7分
(2)当所求直线方程斜率不存在时,直线方程为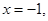 ,与圆相切;
,与圆相切;
当所求直线方程斜率存在时,设直线方程为: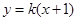 ,
,
因为与圆相切,所以圆心到直线的距离等于半径,
根据点到直线的距离公式得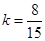 ,
,
所以所求直线方程为 ,
,
综上,所以直线为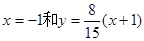 . ……13分
. ……13分
考点:本小题主要考查圆的方程的求解和直线与圆的位置关系的判断和求解,考查学生的运算求解能力.
点评:直线与圆相切时,要注意直线斜率是否存在.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
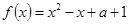
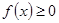 对一切实数
对一切实数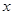 恒成立,求实数
恒成立,求实数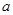 的取值范围.
的取值范围.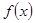 在区间
在区间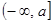 上的最小值
上的最小值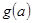 的表达式.
的表达式.
 三点的圆的方程,并指出圆心坐标与圆的半径.
三点的圆的方程,并指出圆心坐标与圆的半径.
 与条件 (1) 的圆相切的直线方程.
与条件 (1) 的圆相切的直线方程. ,且
,且 是垂足,
是垂足,


 的奇偶性;
的奇偶性; 是增函数,求实数
是增函数,求实数 的 取值范围。
的 取值范围。