题目内容

在△ABC中，tan
C
2
=
1
2
，
AH
•
BC
=0，
AB
•(
CA
+
CB
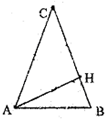
)=0，则过点C，以A、H为两焦点的椭圆的离心率为（　　）
A．
1
2
B．
1
3
C．
2
2
D．
3
3

由已知中
AH
•
BC
=0可得：AH为BC边上的高
又由
AB
•(
CA
+
CB
)=0可得：CA=CB
又由 tan
c
2
=
1
2
，可得tanC=
4
3

令AH=4X，则CH=3X，AC=BC=5X，BH=2X，
则过点C，以A、H为两焦点的椭圆中
2a=5x+3x=8x，2c=4x
则过点B以A、H为两焦点的椭圆的离心率e=
c
a
=
4x
8x
=
1
2

故选A
练习册系列答案
相关题目
已知θ∈（0°，90°]，则方程x2+y2sinθ=1表示的平面图形是（　　）
A．圆B．椭圆C．双曲线D．圆或椭圆
设F1，F2为椭圆
x2
25
+
y2
16
=1的左右焦点，过F1的直线交椭圆于A，B两点，则△ABF2的周长为（　　）
A．28B．26C．22D．20
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点为F，过点F作一条渐近线的垂线，垂足为A，△OAF的面积为
3
2
a2（O为原点），则此双曲线的离心率是（　　）
A．
2
B．2C．
4
3
D．
2
3
3
设A(x1，y1)，B(4，
9
5
)，C(x2，y2)是右焦点为F的椭圆
x2
25
+
y2
9
=1上三个不同的点，则“|AF|，|BF|，|CF|成等差数列”是“x1+x2=8”的（　　）
A．充要条件B．必要不充分条件
C．充分不必要条件D．既非充分也非必要
已知椭圆方程
x2
a2
+
y2
2a-1
=1(1＜a≤5)，过其右焦点做斜率不为0的直线l与椭圆交于A，B两点，设在A，B两点处的切线交于点M（x0，y0），则M点的横坐标x0的取值范围是（　　）
A．[4，+∞）B．[4，
25
4
]		C．(4，
25
4
]		D．(4，
25
4
)
若P是椭圆
x2
4
+
y2
3
=1上的点，F1和F2是焦点，则k=|PF1|•|PF2|的最大值和最小值分别是______和______．
椭圆
y2
16
+
x2
4
=1上一点M到焦点F1的距离为2，N是MF1的中点，O为坐标原点，则|ON|等于（　　）
A．2B．3C．4D．6
已知点P是椭圆
x2
16
+
y2
12
=1(y≠0)上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2平分线上的一点，且F1M⊥MP，则OM的取值范围是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网