题目内容
已知命题p:函数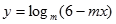 在
在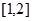 上单调递减.
上单调递减.
⑴求实数m的取值范围;
⑵命题q:方程 在
在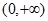 内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
⑴ 1<m<3; ⑵  .
.
解析试题分析:(1)由于u=6-mx中m>0,所以u在[1,2]上是减函数,由复合函数的单调性可知函数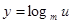 在
在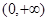 上必是增函数且u=6-mx>0在[1,2]上恒成立;故有m>1且6-2m>0,所以1<m<3;
上必是增函数且u=6-mx>0在[1,2]上恒成立;故有m>1且6-2m>0,所以1<m<3;
(2)由q命题为真可知:函数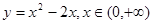 与直线y=-m-1有且只有一交点,由图象得:-m-1=-1或-m-1
与直线y=-m-1有且只有一交点,由图象得:-m-1=-1或-m-1 -1,故有
-1,故有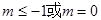 ;再由p或q为真,p且q为假知p与q必然一真一假,从而求得m的取值范围.
;再由p或q为真,p且q为假知p与q必然一真一假,从而求得m的取值范围.
试题解析:.⑴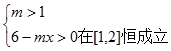 ,
,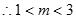
⑵由q命题为真可知:方程 在
在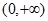 内有一个零点等价于:函数
内有一个零点等价于:函数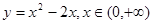 与直线y=-m-1有且只有一交点,由图象得:-m-1=-1或-m-1
与直线y=-m-1有且只有一交点,由图象得:-m-1=-1或-m-1 -1,故有
-1,故有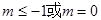 ;又因为p或q为真,p且q为假知p与q必然一真一假,所以有
;又因为p或q为真,p且q为假知p与q必然一真一假,所以有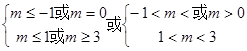 ,所以
,所以 .
.
考点:1.复合函数的单调性,2.函数的零点,3.复合命题真假的判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域是
的定义域是  ,
,  是
是  在
在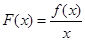 的单调区间。
的单调区间。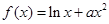 ,求实数a的取值范围
,求实数a的取值范围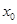 是
是 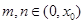 ,求证:
,求证: 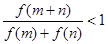 .
.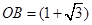 百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设
百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设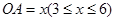 百米,
百米, 百米.
百米.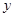 表示成
表示成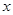 的函数,并求出函数
的函数,并求出函数 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
 有最小正周期2,且当
有最小正周期2,且当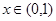 时,
时, .
.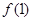 和
和 的值;
的值;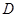 的函数
的函数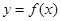 ,若同时满足:
,若同时满足: 在
在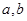 ]
]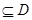 ,使
,使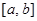 上的值域为
上的值域为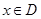 )叫做闭函数.
)叫做闭函数.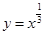 符合条件②的区间
符合条件②的区间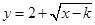 是闭函数,求实数
是闭函数,求实数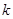 的取值范围.
的取值范围.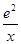 (x>0).
(x>0).
 的反函数的图像过点
的反函数的图像过点 ,则
,则