题目内容
已知函数  的定义域是
的定义域是  ,
,  是
是  的导函数,且
的导函数,且  在
在 上恒成立
上恒成立
(Ⅰ)求函数 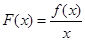 的单调区间。
的单调区间。
(Ⅱ)若函数 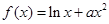 ,求实数a的取值范围
,求实数a的取值范围
(Ⅲ)设 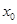 是
是  的零点 ,
的零点 , 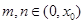 ,求证:
,求证: 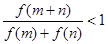 .
.
(Ⅰ)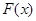 的单增区间是
的单增区间是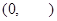 ,无单减区间;(Ⅱ)
,无单减区间;(Ⅱ)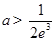 ;(Ⅲ)见解析
;(Ⅲ)见解析
解析试题分析:(Ⅰ)利用导数的运算法则求出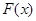 的导数,根据已知条件
的导数,根据已知条件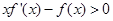 判断出
判断出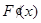 在定义上正负,从而求出
在定义上正负,从而求出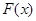 的单调区间;(Ⅱ)求出
的单调区间;(Ⅱ)求出 的导数
的导数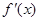 ,将
,将 与
与 代入
代入 ,将条件具体化,根据
,将条件具体化,根据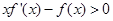 在
在 上恒成立,通过参变分离化为
上恒成立,通过参变分离化为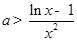 在
在 上恒成立,利用导数求出
上恒成立,利用导数求出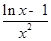 最大值M,从而得出实数a的取值范围a>M;
最大值M,从而得出实数a的取值范围a>M;
(Ⅲ)由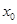 是
是  的零点知,
的零点知,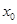 是
是 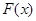 的零点,由(Ⅰ)知
的零点,由(Ⅰ)知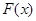 在(0,+
在(0,+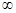 )是单调增函数,得出当
)是单调增函数,得出当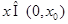 时,
时,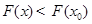 ,即
,即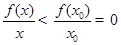 ,即
,即 <0,在利用
<0,在利用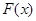 的单调性得出
的单调性得出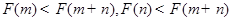 ,利用不等式性质得出
,利用不等式性质得出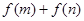 与
与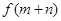 的关系,即可得出所证不等式.
的关系,即可得出所证不等式.
试题解析:(Ⅰ)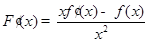
因为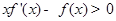 在
在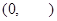 上恒成立
上恒成立
所以 在
在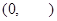 上恒成立
上恒成立
所以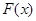 的单增区间是
的单增区间是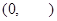 ,无单减区间 (3分)
,无单减区间 (3分)
(Ⅱ)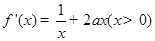
因为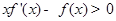 在
在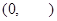 上恒成立
上恒成立
所以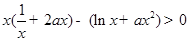 在
在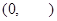 上恒成立
上恒成立
即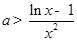 在
在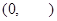 上恒成立 (4分)
上恒成立 (4分)
设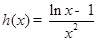 则
则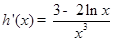
令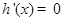 得
得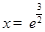
当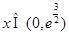 时,
时,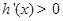 ;当
;当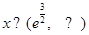 时,
时,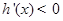
故函数 在
在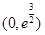 上单调递增,在
上单调递增,在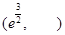 上单调递减,
上单调递减,
所以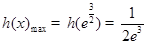 ,所以
,所以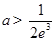

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
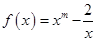 且
且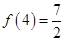 ,
, 的值;
的值; 在
在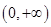 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明.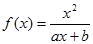 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4. 的值域.
的值域.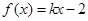 满足
满足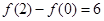 。
。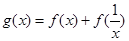 的值域。
的值域。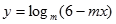 在
在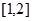 上单调递减.
上单调递减. 在
在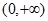 内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.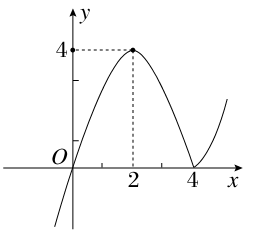
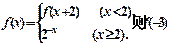 的值为
的值为  ,若
,若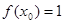 ,则
,则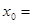 .
.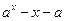 (
(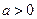 且
且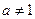 )有两个零点,则实数
)有两个零点,则实数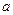 的取值范围是 .
的取值范围是 .