题目内容
等腰梯形ABCD,AB∥CD,DE⊥AB,CF⊥AB,AE=2,沿DE,CF将梯形折叠使A,B重合于A点(如图),G为AC上一点,FG⊥平面ACE.
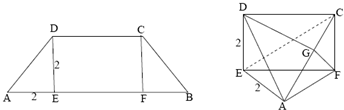
(Ⅰ)求证:AE⊥AF;
(Ⅱ)求DG与平面ACE所成角的正弦值.

(Ⅰ)求证:AE⊥AF;
(Ⅱ)求DG与平面ACE所成角的正弦值.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(I)由FG⊥平面ACE,可得FG⊥AE,由CF⊥AF,CF⊥EF,可得CF⊥平面AEF,可得CF⊥AE,AE⊥平面ACF,即可证明;
(II)如图所示,建立空间直角坐标系.则E(0,0,0),A(
,
,0),C(0,2
,2),D(0,0,2),G(
,
,1).设平面EAC的法向量为
=(x,y,z),则
,设DG与平面ACE所成角为θ,利用sinθ=|cos<
,
>|=
即可得出.
(II)如图所示,建立空间直角坐标系.则E(0,0,0),A(
| 2 |
| 2 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| n |
|
| n |
| EG |
|
| ||||
|
|
解答:
(I)证明:∵FG⊥平面ACE,∴FG⊥AE,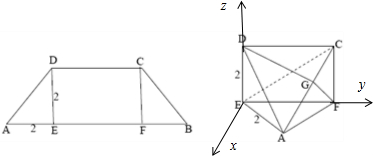
∵CF⊥AF,CF⊥EF,AF∩EF=F,
∴CF⊥平面AEF,
∴CF⊥AE,又FG∩CF=F,
∴AE⊥平面ACF,
∴AE⊥AF;
(II)解:如图所示,建立空间直角坐标系.
则E(0,0,0),A(
,
,0),C(0,2
,2),D(0,0,2),
利用三角形中位线定理与等腰直角三角形的性质可得:G(
,
,1).
∴
=(
,
,-1),
=(
,
,0),
=(0,2
,2).
设平面EAC的法向量为
=(x,y,z),则
,
令y=-1,解得x=1,z=
.
∴
=(1,-1,
).
设DG与平面ACE所成角为θ.
则sinθ=|cos<
,
>|=
=
=
.

∵CF⊥AF,CF⊥EF,AF∩EF=F,
∴CF⊥平面AEF,
∴CF⊥AE,又FG∩CF=F,
∴AE⊥平面ACF,
∴AE⊥AF;
(II)解:如图所示,建立空间直角坐标系.
则E(0,0,0),A(
| 2 |
| 2 |
| 2 |
利用三角形中位线定理与等腰直角三角形的性质可得:G(
| ||
| 2 |
3
| ||
| 2 |
∴
| DG |
| ||
| 2 |
3
| ||
| 2 |
| EA |
| 2 |
| 2 |
| EC |
| 2 |
设平面EAC的法向量为
| n |
|
令y=-1,解得x=1,z=
| 2 |
∴
| n |
| 2 |
设DG与平面ACE所成角为θ.
则sinθ=|cos<
| n |
| EG |
|
| ||||
|
|
2
| ||
2
|
| ||
| 3 |
点评:本题考查了空间线面面面位置关系的判定及其性质、空间角的求法、等腰直角三角形的性质、三角形的中位线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
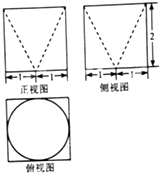

A、
| ||
B、
| ||
C、8-
| ||
D、8-
|
已知一组数1,1,2,3,5,8,x,21,34,55,按这组数规律,x应为( )
| A、11 | B、12 | C、13 | D、14 |
七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙,丙两位同学要站在一起,则不同的排法有( )
| A、240种 | B、192种 |
| C、120种 | D、96种 |
已知函数f(x)=kx-1,其中实数k随机选自区间[-2,2],?x∈[0,1],f(x)≤0的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|