题目内容
如图，测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=15°，∠BDC=30°，CD=30，并在点C测得塔顶A的仰角为60°，则塔高AB=
- A.
- B.
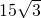
- C.
- D.
D
分析：先根据三角形内角和为180°，求得∠CBD，再根据正弦定理求得BC，进而在Rt△ABC中，根据AB=BCtan∠ACB求得AB
解答：在△BCD中，∠CBD=180°-15°-30°=135°．
由正弦定理得
，所以BC=15
．
在Rt△ABC中，AB=BCtan∠ACB=15×
=．
故选D．
点评：本题考查了解三角形的实际应用，考查学生的计算能力，属于基础题．
分析：先根据三角形内角和为180°，求得∠CBD，再根据正弦定理求得BC，进而在Rt△ABC中，根据AB=BCtan∠ACB求得AB
解答：在△BCD中，∠CBD=180°-15°-30°=135°．
由正弦定理得
，所以BC=15．在Rt△ABC中，AB=BCtan∠ACB=15
×=．故选D．
点评：本题考查了解三角形的实际应用，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=75°，∠BDC=60°，CD=60米，并在点C测得塔顶A的仰角为60°，则塔高AB=（ ）
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D．现测得∠BCD=α，∠BDC=β，CD=s，并在点C测得塔顶A的仰角为θ，则塔高AB=
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，现测得∠BCD=45°，∠BDC=60°，CD=10m，并在点C测得塔顶A的仰角为45°，则塔高AB=
如图，测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=15°，∠BDC=30°，CD=30，并在点C测得塔顶A的仰角为60°，则塔高AB=（ ）
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D．测得∠BDC=30°，CD=30米，并在点C测得塔顶A的仰角为60°，