题目内容
若函数
(1)若f(x)在[1,+∞)上为增函数,求m的范围.
(2)当m=1时,若a>b>1,比较f(aabb4a)与f[(a+b)a+b]的大小,并说明理由.
(3)当m=1时,设{an}为正项数列,且n≥2时[f′(an)•f′(an-1)+
 ]•an2=q,(其中q≥2010),an的前n项和为Sn,
]•an2=q,(其中q≥2010),an的前n项和为Sn, ,若bn≥2011n恒成立,求q的最小值.
,若bn≥2011n恒成立,求q的最小值.
【答案】分析:(1)由f(x)= ,知
,知 =
= ,x>0.由f(x)在[1,+∞)上为增函数,知x∈[1,+∞)时,
,x>0.由f(x)在[1,+∞)上为增函数,知x∈[1,+∞)时, 恒成立.由此能导出m的范围.
恒成立.由此能导出m的范围.
(2)当m=1时, ,x∈[1,+∞)时,
,x∈[1,+∞)时, ,f(x)在[1,+∞)上单调递增,要比较f(aaba4a)与f[(a+b)a+b]的大小,即比较
,f(x)在[1,+∞)上单调递增,要比较f(aaba4a)与f[(a+b)a+b]的大小,即比较 与
与 的大小.由此能推导出f(aabb4a)>f[(a+b)a+b].
的大小.由此能推导出f(aabb4a)>f[(a+b)a+b].
(3)当m=1时, ,且
,且 ,所以
,所以 ,由
,由 恒成立,q≥2010时,数列
恒成立,q≥2010时,数列 为单调递减数列,能够推导出若bn≥2011n恒成立,求q的最小值.
为单调递减数列,能够推导出若bn≥2011n恒成立,求q的最小值.
解答:解:(1)∵f(x)= ,
,
∴
= ,x>0.
,x>0.
∵f(x)在[1,+∞)上为增函数,
∴ 在[1,+∞)上恒大于或等于0,
在[1,+∞)上恒大于或等于0,
即:x∈[1,+∞)时, 恒成立.
恒成立.
又∵m∈R+,即:mx-1≥0恒成立.即: 恒成立.
恒成立.
∴m的范围为:[1,+∞).…(4分)
(2)当m=1时, ,x∈[1,+∞)时,
,x∈[1,+∞)时, ,
,
∴f(x)在[1,+∞)上单调递增,
要比较f(aaba4a)与f[(a+b)a+b]的大小,
∵aabb4a>1,且(a+b)a+b>1,
即比较aabb4a与(a+b)a+b的大小.
即比较 与
与 的大小.
的大小.
∴ -
-
=alog2a+blog2b+2a-(a+b)log2(a+b)
=alog2a+2a-alog2(a+b)-blog2(a+b)+blog2b,
设g(x)=xlog2x+2x-xlog2(x+b)+blog2b,x∈(b,+∞),
 -
-
=log2x+2-log2(x+b)
= .
.
∵x>b,
∴g′(x)>0,∴g(x)在(b,+∞)单调递增.
且a>b,
∴g(a)>g(b),
即:alog2a+2a-alog2(a+b)-blog2(a+b)+blog2b>0,
∴ ,
,
∴f(aabb4a)>f[(a+b)a+b].
(3)当m=1时, ,
,
且 ,
,
∴ ,
,
∴ ,
,
∴ .
.
由: =
= ,q≥2010,
,q≥2010,
∵bn≥2011n恒成立,
即: 恒成立,
恒成立,
显然,q≥2010时,数列 为单调递减数列,
为单调递减数列,
且 ,
,
当q≥2011时, 中的每一项都大于2011,
中的每一项都大于2011,
∴ 恒成立,
恒成立,
当q∈[2010,2011)时,由 数列 为单调递减数列,
为单调递减数列,
且 ,
,
说明数列 在有限项后必定小于2011,
在有限项后必定小于2011,
设 ,
,
且数列{Mn}也为单调递减数列,M1≥0,
根据以上分析:数列 中必有一项,
中必有一项,
(设为第k项) ,(其中Mk≥0,且Mk+1<0),
,(其中Mk≥0,且Mk+1<0),
∵{Mn}为单调递减数列,
∴ +…+
+…+
=2011n+M1+M2+…+Mk+Mk+1+…+Mn
≤2011n+kM1+Mk+1+…+Mn
≤2011n+kM1+(n-k)Mk+1,
当n→∞时,kM1+(n-k)Mk+1<0,
∴ ,
,
∴q∈[2010,2011)时,不满足条件.
综上所得:qmin=2011.…(14分)
点评:本题考查数列与不等式的综合应用,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易错点是数列 中必有一项,(设为第k项)
中必有一项,(设为第k项) ,(其中Mk≥0,且Mk+1<0)的推导过程.
,(其中Mk≥0,且Mk+1<0)的推导过程.
 ,知
,知 =
= ,x>0.由f(x)在[1,+∞)上为增函数,知x∈[1,+∞)时,
,x>0.由f(x)在[1,+∞)上为增函数,知x∈[1,+∞)时, 恒成立.由此能导出m的范围.
恒成立.由此能导出m的范围.(2)当m=1时,
 ,x∈[1,+∞)时,
,x∈[1,+∞)时, ,f(x)在[1,+∞)上单调递增,要比较f(aaba4a)与f[(a+b)a+b]的大小,即比较
,f(x)在[1,+∞)上单调递增,要比较f(aaba4a)与f[(a+b)a+b]的大小,即比较 与
与 的大小.由此能推导出f(aabb4a)>f[(a+b)a+b].
的大小.由此能推导出f(aabb4a)>f[(a+b)a+b].(3)当m=1时,
 ,且
,且 ,所以
,所以 ,由
,由 恒成立,q≥2010时,数列
恒成立,q≥2010时,数列 为单调递减数列,能够推导出若bn≥2011n恒成立,求q的最小值.
为单调递减数列,能够推导出若bn≥2011n恒成立,求q的最小值.解答:解:(1)∵f(x)=
 ,
,∴

=
 ,x>0.
,x>0.∵f(x)在[1,+∞)上为增函数,
∴
 在[1,+∞)上恒大于或等于0,
在[1,+∞)上恒大于或等于0,即:x∈[1,+∞)时,
 恒成立.
恒成立.又∵m∈R+,即:mx-1≥0恒成立.即:
 恒成立.
恒成立.∴m的范围为:[1,+∞).…(4分)
(2)当m=1时,
 ,x∈[1,+∞)时,
,x∈[1,+∞)时, ,
,∴f(x)在[1,+∞)上单调递增,
要比较f(aaba4a)与f[(a+b)a+b]的大小,
∵aabb4a>1,且(a+b)a+b>1,
即比较aabb4a与(a+b)a+b的大小.
即比较
 与
与 的大小.
的大小.∴
 -
-
=alog2a+blog2b+2a-(a+b)log2(a+b)
=alog2a+2a-alog2(a+b)-blog2(a+b)+blog2b,
设g(x)=xlog2x+2x-xlog2(x+b)+blog2b,x∈(b,+∞),
 -
-
=log2x+2-log2(x+b)
=
 .
.∵x>b,
∴g′(x)>0,∴g(x)在(b,+∞)单调递增.
且a>b,
∴g(a)>g(b),
即:alog2a+2a-alog2(a+b)-blog2(a+b)+blog2b>0,
∴
 ,
,∴f(aabb4a)>f[(a+b)a+b].
(3)当m=1时,
 ,
,且
 ,
,∴
 ,
,∴
 ,
,∴
 .
.由:
 =
= ,q≥2010,
,q≥2010,∵bn≥2011n恒成立,
即:
 恒成立,
恒成立,显然,q≥2010时,数列
 为单调递减数列,
为单调递减数列,且
 ,
,当q≥2011时,
 中的每一项都大于2011,
中的每一项都大于2011,∴
 恒成立,
恒成立,当q∈[2010,2011)时,由 数列
 为单调递减数列,
为单调递减数列,且
 ,
,说明数列
 在有限项后必定小于2011,
在有限项后必定小于2011,设
 ,
,且数列{Mn}也为单调递减数列,M1≥0,
根据以上分析:数列
 中必有一项,
中必有一项,(设为第k项)
 ,(其中Mk≥0,且Mk+1<0),
,(其中Mk≥0,且Mk+1<0),∵{Mn}为单调递减数列,
∴
 +…+
+…+
=2011n+M1+M2+…+Mk+Mk+1+…+Mn
≤2011n+kM1+Mk+1+…+Mn
≤2011n+kM1+(n-k)Mk+1,
当n→∞时,kM1+(n-k)Mk+1<0,
∴
 ,
,∴q∈[2010,2011)时,不满足条件.
综上所得:qmin=2011.…(14分)
点评:本题考查数列与不等式的综合应用,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易错点是数列
 中必有一项,(设为第k项)
中必有一项,(设为第k项) ,(其中Mk≥0,且Mk+1<0)的推导过程.
,(其中Mk≥0,且Mk+1<0)的推导过程. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
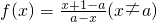
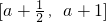 时,求f(x)的值域;
时,求f(x)的值域;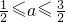 ,求g(x)的最小值.
,求g(x)的最小值.