题目内容
(本小题满分13分)
已知函数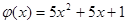
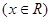 ,函数
,函数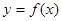 的图象与
的图象与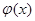 的图象关于点
的图象关于点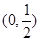 中心对称。
中心对称。
(1)求函数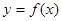 的解析式;
的解析式;
(2)如果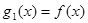 ,
,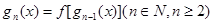 ,试求出使
,试求出使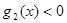 成立的
成立的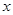 取值范围;
取值范围;
(3)是否存在区间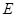 ,使
,使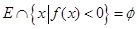 对于区间内的任意实数
对于区间内的任意实数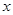 ,只要
,只要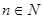 且
且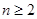 时,都有
时,都有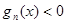 恒成立?
恒成立?
已知函数
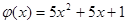
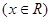 ,函数
,函数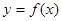 的图象与
的图象与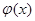 的图象关于点
的图象关于点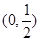 中心对称。
中心对称。(1)求函数
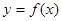 的解析式;
的解析式;(2)如果
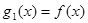 ,
,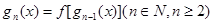 ,试求出使
,试求出使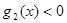 成立的
成立的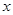 取值范围;
取值范围;(3)是否存在区间
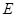 ,使
,使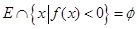 对于区间内的任意实数
对于区间内的任意实数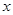 ,只要
,只要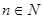 且
且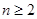 时,都有
时,都有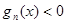 恒成立?
恒成立?解:(1)
(2)由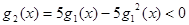 解得
解得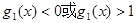
即
解得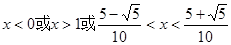
(3)由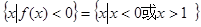 ,
,
又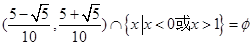 ,
,
当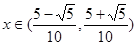 时,
时,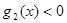 ,
,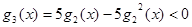 ,
,
∴对于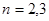 时,
时,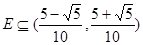 ,命题成立。
,命题成立。
以下用数学归纳法证明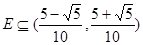 对
对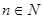 ,且
,且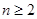 时,都有
时,都有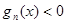 成立
成立
假设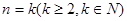 时命题成立,即
时命题成立,即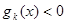 ,
,
那么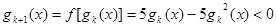 即
即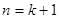 时,命题也成立。
时,命题也成立。
∴存在满足条件的区间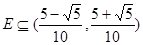 。
。

(2)由
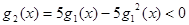 解得
解得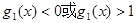
即

解得
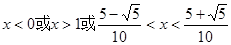
(3)由
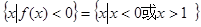 ,
,又
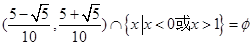 ,
,当
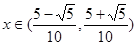 时,
时,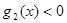 ,
,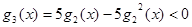 ,
,∴对于
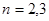 时,
时,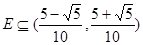 ,命题成立。
,命题成立。以下用数学归纳法证明
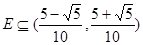 对
对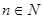 ,且
,且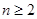 时,都有
时,都有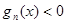 成立
成立假设
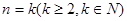 时命题成立,即
时命题成立,即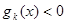 ,
,那么
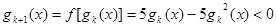 即
即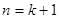 时,命题也成立。
时,命题也成立。∴存在满足条件的区间
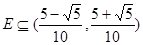 。
。略

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
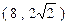 ,求出函数解析式,并指出函数的单调性与奇偶性。
,求出函数解析式,并指出函数的单调性与奇偶性。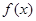 是定义在
是定义在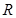 上不恒为
上不恒为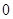 的函数,且对于任意的实数
的函数,且对于任意的实数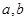 满足
满足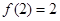 ,
,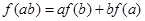 ,
,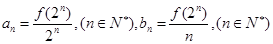 ,考察下列结论:①
,考察下列结论:①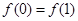 ②
②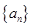 为等差数列 ④数列
为等差数列 ④数列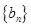 为等比数列,其中正确的个数为( )
为等比数列,其中正确的个数为( )




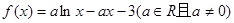
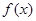 的单调区间;
的单调区间;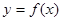 的图像在点
的图像在点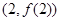 处的切线的斜率为
处的切线的斜率为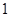 ,问:
,问: 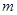 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的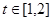 ,函数
,函数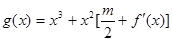 在区间
在区间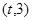 上总存在极值?
上总存在极值?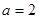 时,设函数
时,设函数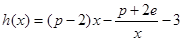 ,若在区间
,若在区间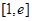 上至少存在一个
上至少存在一个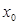 ,使得
,使得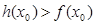 成立,试求实数
成立,试求实数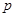 的取值范围.
的取值范围.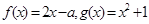 ,
,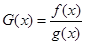 ,
,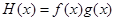 .
.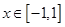 ,求使
,求使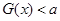 恒成立的
恒成立的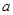 的取值范围;
的取值范围;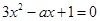 的两根为
的两根为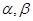 (
(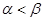 ),且函数
),且函数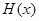 在区间
在区间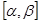 上的最大值与最小值之差是8,求
上的最大值与最小值之差是8,求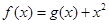 ,曲线
,曲线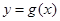 在点
在点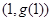 处的切线方程为
处的切线方程为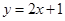 ,则曲线
,则曲线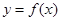 在点
在点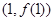 处切线的斜率为 ( )
处切线的斜率为 ( )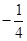
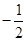
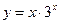 在点
在点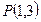 处的切线方程为
处的切线方程为 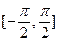 上的任意x1、x2,有如下条件:①x1>x2;②|x1|>|x2|;③x13>x23;④x12>x22;⑤|x1|>x2,其中能使f(x1)>f(x2)恒成立的条件的序号是 ;
上的任意x1、x2,有如下条件:①x1>x2;②|x1|>|x2|;③x13>x23;④x12>x22;⑤|x1|>x2,其中能使f(x1)>f(x2)恒成立的条件的序号是 ;