题目内容
已知椭圆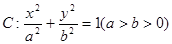 经过点
经过点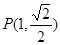 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)动直线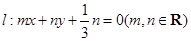 交椭圆
交椭圆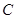 于
于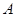 、
、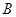 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点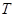 ,使得以
,使得以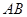 为直径的圆恒过点
为直径的圆恒过点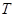 .若存在,求出点
.若存在,求出点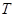 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
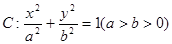 经过点
经过点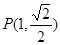 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形.(Ⅰ)求椭圆的方程;
(Ⅱ)动直线
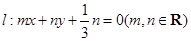 交椭圆
交椭圆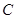 于
于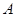 、
、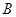 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点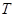 ,使得以
,使得以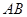 为直径的圆恒过点
为直径的圆恒过点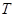 .若存在,求出点
.若存在,求出点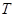 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(1) (2)点
(2)点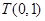 就是所求的点
就是所求的点
 (2)点
(2)点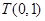 就是所求的点
就是所求的点试题分析:(Ⅰ)椭圆
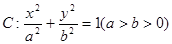 的两焦点与短轴的一个端点连线构成等腰直角三角形,所以
的两焦点与短轴的一个端点连线构成等腰直角三角形,所以 ,故椭圆的方程为
,故椭圆的方程为 .
.又因为椭圆经过点
 ,代入可得
,代入可得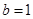 ,2分
,2分所以
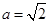 ,故所求椭圆方程为
,故所求椭圆方程为 .4分
.4分(Ⅱ)当直线
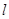 的斜率为0时,直线
的斜率为0时,直线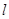 为
为 ,直线
,直线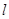 交椭圆
交椭圆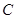 于
于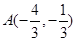 、
、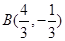 两点,以
两点,以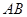 为直径的圆的方程为
为直径的圆的方程为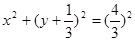 ;
; 当直线
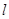 的斜率不存在时,直线
的斜率不存在时,直线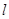 为
为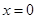 ,直线
,直线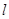 交椭圆
交椭圆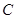 于
于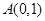 、
、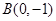 两点,以
两点,以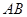 为直径的圆的方程为
为直径的圆的方程为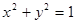 ,
, 由
 解得
解得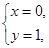
即两圆相切于点
 ,因此,所求的点
,因此,所求的点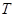 如果存在,只能是
如果存在,只能是 .8分
.8分事实上,点
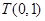 就是所求的点.
就是所求的点.证明如下:
当
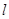 的斜率不存在时,以
的斜率不存在时,以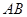 为直径的圆过点
为直径的圆过点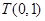 .9分
.9分若
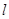 的斜率存在时,可设直线
的斜率存在时,可设直线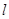 为
为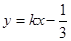 ,
,由
 消去
消去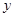 得
得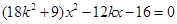 .
.记点
 、
、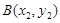 ,则
,则 10分
10分又因为
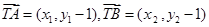 ,
,所以
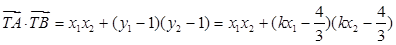

 .
.所以
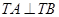 ,即以
,即以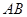 为直径的圆恒过点
为直径的圆恒过点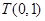 ,12分
,12分所以在坐标平面上存在一个定点
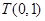 满足条件.13分
满足条件.13分点评:主要是考查了解析几何中运用代数的方法来建立方程组结合韦达定理来研究位置关系的运用,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
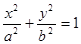
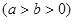 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点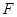 的最短距离为
的最短距离为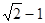 .
.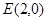 且斜率为
且斜率为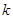 (
(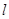 与C交于
与C交于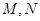 两点,
两点,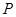 是点
是点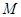 关于
关于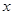 轴的对称点,证明:
轴的对称点,证明: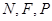 三点共线.
三点共线.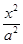 +
+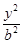 =1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=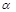 , 且
, 且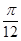 ,
,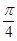 ], 则该椭圆离心率的取值范围为 ( )
], 则该椭圆离心率的取值范围为 ( ) ,1 )
,1 ) 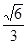 ]
]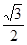
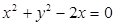 ,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 __________;
,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 __________;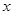 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为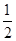 ,则
,则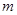 的值为( )
的值为( )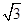
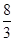
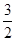
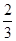
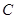 过定点
过定点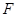
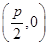 ,且与直线
,且与直线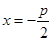 相切,其中
相切,其中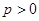 .设圆心
.设圆心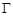 的程为
的程为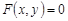
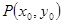 (
(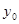
 0) ,方向向量
0) ,方向向量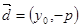 的直线
的直线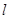 (不过P点)与曲线
(不过P点)与曲线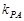 ,
,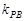 ,计算
,计算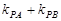 ;
;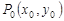 、
、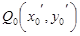 ,分别过点
,分别过点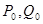 作倾斜角互补的两条直线
作倾斜角互补的两条直线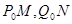 分别与曲线
分别与曲线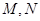 两点,求证直线
两点,求证直线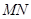 的斜率为定值;
的斜率为定值;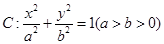 的离心率为
的离心率为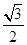 .双曲线
.双曲线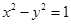 的渐近线与椭圆
的渐近线与椭圆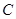 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆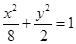


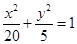
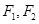 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P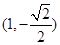 在椭圆上,线段
在椭圆上,线段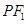 与y轴的交点M满足
与y轴的交点M满足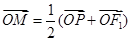
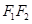 为直径的圆,直线
为直径的圆,直线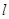 :
: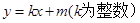 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点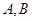 ,当
,当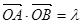 ,且满足
,且满足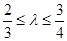 时,求直线
时,求直线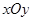 中,已知△ABC顶点
中,已知△ABC顶点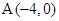 和
和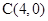 ,顶点B在椭圆
,顶点B在椭圆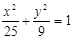 上,则
上,则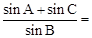 .
.