题目内容
函数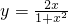
- A.（-∞，+∞）上是单调递增函数
- B.（-∞，+∞）上是单调减函数
- C.[-1，1]上是单调增函数，（-∞，-1）和（1，+∞）上分别是单调减函数
- D.[-1，1]上是单调减函数，（-∞，-1）和（1，+∞）上分别是单调增函数
C
分析：先求导函数，由y′＞0，可得函数的单调增区间；由y′＜0，可得函数的单调减区间．
解答：由题意，
，
由y′＞0，可得x∈（-1，1）；由y′＜0，可得x＜-1，或x＞1；
∴[-1，1]上是单调增函数，（-∞，-1）和（1，+∞）上分别是单调减函数
故选C．
点评：本题以函数为载体，考查函数的单调性，考查导数的运用，属于基础题．
分析：先求导函数，由y′＞0，可得函数的单调增区间；由y′＜0，可得函数的单调减区间．
解答：由题意，
，由y′＞0，可得x∈（-1，1）；由y′＜0，可得x＜-1，或x＞1；
∴[-1，1]上是单调增函数，（-∞，-1）和（1，+∞）上分别是单调减函数
故选C．
点评：本题以函数为载体，考查函数的单调性，考查导数的运用，属于基础题．
练习册系列答案
相关题目
图中三条曲线给出了三个函数的图象，一条表示汽车位移函数s（t），一条表示汽车速度函数v（t），一条是汽车加速度函数a（t），则（ ）