题目内容
16.数列{an}前n项和为Sn,其中Sn是首项为5,公比为5的等比数列,则an=$\left\{\begin{array}{l}{5,n=1}\\{{5}^{n}-{5}^{n-1},n≥2}\end{array}\right.$.分析 由等比数列性质先求出Sn,再由公式${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$能求出结果.
解答 解:∵数列{an}前n项和为Sn,其中Sn是首项为5,公比为5的等比数列,
∴${S}_{n}={5}^{n}$,
∴a1=S1=5,
n≥2时,an=Sn-Sn-1=5n-5n-1,
n=1时,上式不成立,
∴${a}_{n}=\left\{\begin{array}{l}{5,n=1}\\{{5}^{n}-{5}^{n-1},n≥2}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{5,n=1}\\{{5}^{n}-{5}^{n-1},n≥2}\end{array}\right.$.
点评 本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
10.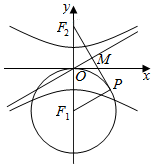 如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )
如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )
 如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )
如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
8.广丰一中现有职工180人,其中高级职称42人,中级职称78人,一般职员60人,现抽取30人进行分层抽样,则各职称人数分别为( )
| A. | 5,15,10 | B. | 3,18,9 | C. | 7,13,10 | D. | 5,16,9 |
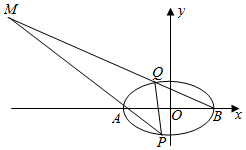 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{3}$,且椭圆的四个顶点相连得到的凸四边形的面积为12$\sqrt{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{3}$,且椭圆的四个顶点相连得到的凸四边形的面积为12$\sqrt{2}$.