题目内容
数列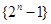 的前
的前 项组成集合
项组成集合 ,从集合
,从集合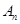 中任取
中任取 个数,其所有可能的
个数,其所有可能的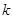 个数的乘积的和为
个数的乘积的和为 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
, ;当
;当 时,
时, ,
, ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想 ,并用数学归纳法证明.
,并用数学归纳法证明.
(Ⅰ)63; (Ⅱ) .
.
解析试题分析:(Ⅰ)通过列举进行计算;(Ⅱ)先从特殊入手,
当 时,
时, ,
, ,
, ;
;
当 时,
时, ,
, ,
, ,所以
,所以 ;
;
从特殊到一般探求 与
与 之间的递推关系,从而便于用数学归纳法证明.
之间的递推关系,从而便于用数学归纳法证明.
试题解析:(Ⅰ)当 时,
时, ,
, ,
, ,所以
,所以 ;
;
(Ⅱ)由 ,
,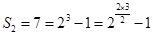 ,
,
猜想 ,下面证明:
,下面证明:
(1)易知 时成立;
时成立;
(2)假设 时
时 ,
,
则 时,
时,

(其中 ,为
,为 时可能的
时可能的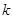 个数的乘积的和为
个数的乘积的和为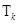 ),
),




即 时
时 也成立,
也成立,
综合(1)(2)知对 ,
, 成立.
成立.
所以 .
.
考点:归纳推理、数学归纳法.

练习册系列答案
相关题目
复数 (其中
(其中 为虚数单位)的虚部是 ( )
为虚数单位)的虚部是 ( )
A. | B. | C.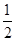 | D. |
 是一个自然数,
是一个自然数, 是
是 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; ,使得
,使得 .
. ,且
,且 ,求证:
,求证:

 +
+ n5+
n5+ n4+
n4+ n3-
n3- n.
n. ,考查
,考查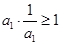 ;
; ;
; .
. 都成立的类似不等式,并用数学归纳法加以证明.
都成立的类似不等式,并用数学归纳法加以证明.


