题目内容
投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n﹣mi)为实数的概率为( )
A. | B. | C. | D. |
C
解析试题分析:因为(m+ni)(n-mi)=2mn+(n2-m2)i为实数所以n2=m2,
故m=n则可以取1、2、3、4、5、6,共6种可能,
所以P= ,故选C.
,故选C.
考点:1.基本概念;2.古典概型及其概率计算公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 为纯虚数,
为纯虚数, 是实数,那么
是实数,那么 ( )
( )
A. | B. | C. | D. |
若 ,其中
,其中 ,
, 是虚数单位,则
是虚数单位,则 = ( )
= ( )
A. | B. | C. | D. |
“a = 1”是“复数 (
( ,i为虚数单位)是纯虚数”的 ( )
,i为虚数单位)是纯虚数”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 是虚数单位),则
是虚数单位),则 ( )
( )
A. | B. | C. | D. |
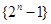 的前
的前 项组成集合
项组成集合 ,从集合
,从集合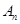 中任取
中任取 个数,其所有可能的
个数,其所有可能的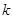 个数的乘积的和为
个数的乘积的和为 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
, ;当
;当 时,
时, ,
, ,
, .
. ;
; ,并用数学归纳法证明.
,并用数学归纳法证明. 使得关于n的等式
使得关于n的等式
