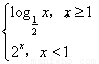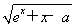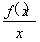Question

已知函数f(x)＝lnx－ax2＋(2－a)x.

(1)讨论f(x)的单调性；

(2)设a>0，证明：当0<x<时，f>f；

(3)若函数y＝f(x)的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明：＜0.

 

Answer 1

（1）在上单调递增，在上是减函数（2）见解析（3）见解析

【解析】(1)【解析】
f(x)的定义域为(0，＋∞),

f′(x)＝－2ax＋(2－a)＝－.

①若a≤0，则f′(x)>0，所以f(x)在(0，＋∞)上是增函数．

②若a>0，则由f′(x)＝0得x＝，且当x∈时，f′(x)>0，当x>时，f′(x)<0.所以f(x)在上单调递增，在上是减函数.

(2)【解析】
设函数g(x)＝f－f，

则g(x)＝ln(1＋ax)－ln(1－ax)－2ax，

g′(x)＝－2a＝.

当0<x<时，g′(x)>0，而g(0)＝0，所以g(x)>0.

故当0<x<时，f>f.

(3)证明：由(1)可得，当a≤0时，函数y＝f(x)的图象与x轴至多有一个交点，

故a>0，从而f(x)的最大值为f，且f>0.

不妨设A(x1，0)，B(x2，0)，0<x1<x2，则0<x1<<x2.

由(2)得f＝f>f(x1)＝0.

从而x2>－x1，于是x0＝>.由(1)知，f′(x0)<0