题目内容
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1) 若l在两坐标轴上截距相等,求l的方程;
(2) 若l不经过第二象限,求实数a的取值范围.
解:(1) 当直线过原点时,该直线在x轴和y轴上的截距均为零,
∴ a=2,即方程为3x+y=0符合题意.当直线不过原点时,由截距存在且均不为0,
∴ =a-2,即a+1=1,
=a-2,即a+1=1,
∴ a=0,即方程为x+y+2=0.
(2) (解法1)将l的方程化为y=-(a+1)x+a-2,
∴
∴ a≤-1.综上可知a的取值范围是a≤-1.
(解法2)将l的方程化为(x+y+2)+a(x-1)=0(a∈R).它表示过l1:x+y+2=0与l2:x-1=0交点(1,-3)的直线系(不包括x=1).由图象可知l的斜率-(a+1)≥0,即a≤-1时,直线l不经过第二象限.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 与抛物线
与抛物线 相切,则
相切,则
 ,
, ,设函数
,设函数 ,
, 的零点均在区间
的零点均在区间 内,则
内,则 的最小值为( )
的最小值为( ) B.
B. C.
C.  D.
D. 
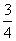 (x-2),则该直线另外三种特殊形式的方程为______________,______________,______________.
(x-2),则该直线另外三种特殊形式的方程为______________,______________,______________. ,求直线AB的倾斜角α的取值范围.
,求直线AB的倾斜角α的取值范围. (
( )的单调递增区间是_____________________.
)的单调递增区间是_____________________. ,集合
,集合 ,则
,则 =( ).
=( ). (B)
(B) (C)
(C) (D)
(D)

 ,
, ,那么命题
,那么命题 为( )
为( )  B.
B.
 D.
D.