题目内容
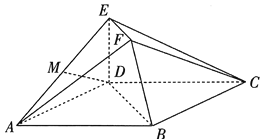
【题目】图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是（ ）
A. 捕食者和被捕食者数量与时间以
年为周期
B. 由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少
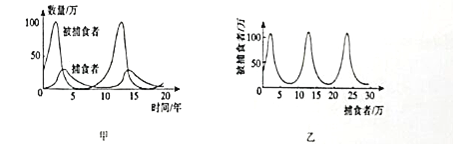
C. 捕食者和被捕食者数量之间的关系可以用图1乙描述
D. 捕食者的数量在第
年和
年之间数量在急速减少
【答案】C
【解析】分析：由题意可知：捕食者和被捕食者数量与时间以10年为周期呈周期性变化，故捕食者和被捕食者数量之间的关系应为环状，进而得到答案
详解：由已知中某理想状态下捕食者和被捕食者数量随时间的变化规律．
可得捕食者和被捕食者数量与时间以10年为周期呈周期性变化，
捕食者的数量在第25年和30年之间数量在急速减少，正确；
由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少，
故捕食者和被捕食者数量之间的关系应为环状，
捕食者和被捕食者数量之间的关系可以用图1乙描述，显然不正确；
故选：C．
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表：
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得： 
， 
， 
， 
，
，线性回归模型的残差平方和
，e8.0605≈3167，其中xi, yi分别为观测数据中的温度和产卵数，i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型，求y关于x的回归方程
=
x+
（精确到0.1）；
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为
=0.06e0.2303x，且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比，用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数（结果取整数）.
附：一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线
=
x+
的斜率和截距的最小二乘估计为
=
；相关指数R2=
．
【题目】某大学生从全校学生中随机选取
名统计他们的鞋码大小，得到如下数据：
鞋码 |
|
|
|
|
|
|
|
|
|
| 合计 |
男生 |
|
|
|
|
|
|
|
|
| ||
女生 |
|
|
|
|
|
|
|
|
|
以各性别各鞋码出现的频率为概率．
（
）从该校随机挑选一名学生，求他（她）的鞋码为奇数的概率．
（
）为了解该校学生考试作弊的情况，从该校随机挑选
名学生进行抽样调查．每位学生从装有除颜色外无差别的
个红球和
个白球的口袋中，随机摸出两个球，若同色，则如实回答其鞋码是否为奇数；若不同色，则如实回答是否曾在考试中作弊．这里的回答，是指在纸上写下“是”或“否”．若调查人员回收到
张“是”的小纸条，试估计该校学生在考试中曾有作弊行为的概率．
