题目内容
设函数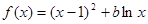 ,其中
,其中 为常数.
为常数.
(Ⅰ)当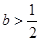 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当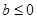 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;
(Ⅲ)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.
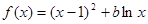 ,其中
,其中 为常数.
为常数.(Ⅰ)当
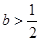 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;(Ⅱ)当
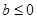 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;(Ⅲ)求证对任意不小于3的正整数
 ,不等式
,不等式 都成立.
都成立.(1)当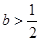 时,
时,  ,函数
,函数 在定义域
在定义域 上单调递增
上单调递增
(2) 时,
时, 有惟一极小值点
有惟一极小值点 ,
,
(3)由(2)可知当 时,函数
时,函数 ,此时
,此时 有惟一极小值点
有惟一极小值点 故可以得到函数
故可以得到函数 借助于单调性来证明不等式。
借助于单调性来证明不等式。
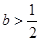 时,
时,  ,函数
,函数 在定义域
在定义域 上单调递增
上单调递增(2)
 时,
时, 有惟一极小值点
有惟一极小值点 ,
,(3)由(2)可知当
 时,函数
时,函数 ,此时
,此时 有惟一极小值点
有惟一极小值点 故可以得到函数
故可以得到函数 借助于单调性来证明不等式。
借助于单调性来证明不等式。试题分析:解:(1)由题意知,
 的定义域为
的定义域为 ,
,
 当
当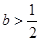 时,
时,  ,函数
,函数 在定义域
在定义域 上单调递增. …………4分
上单调递增. …………4分(2)当
 时
时 有两个不同解,
有两个不同解,

 ,
, ,
,此时
 ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表: |  |  |  |
 |  |  |  |
 | 减 | 极小值 | 增 |
 时,
时, 有惟一极小值点
有惟一极小值点 , ………8分
, ………8分 (3)由(2)可知当
 时,函数
时,函数 ,
,此时
 有惟一极小值点
有惟一极小值点
且

 …… 11分
…… 11分令函数


 13分
13分点评:主要是考查了导数在研究函数中的运用,以及函数的极值,以及函数与不等式的综合运用,属于难度题。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 ,
,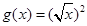
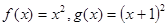
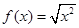 ,
,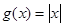
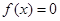 ,
,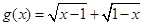
 ,则
,则 _____________
_____________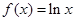 ,
,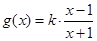
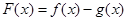 的单调区间;
的单调区间;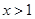 时,函数
时,函数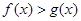 恒成立,求实数
恒成立,求实数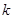 的取值范围;
的取值范围;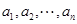 满足
满足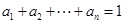 .求证:
.求证: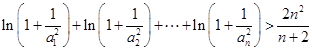 .
. ,
, ,
, ,则( )
,则( )



 与
与
 与
与
 与
与
 与
与
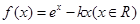
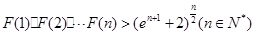 .
.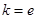 ,试确定函数
,试确定函数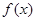 的单调区间;
的单调区间;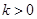 且对任意
且对任意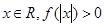 恒成立,试确定实数
恒成立,试确定实数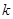 的取值范围;
的取值范围;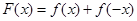 ,求证:
,求证: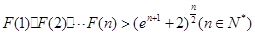 .
.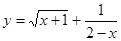 的定义域是 。
的定义域是 。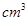 ,高为2
,高为2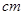 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?