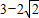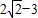题目内容
设点P(x,y)是圆x2+y2=1外一点,PS,PT是圆的两条切线,S,T是切点.则
•
的最小值为( )
| PS |
| PT |
分析:利用圆切线的性质:与圆心切点连线垂直;设出一个角,通过解直角三角形求出PS,PT的长;利用向量的数量积公式表示出
•
,利用三角函数的二倍角公式化简函数,再通过换元,利用基本不等式求出最值.
| PS |
| PT |
解答:解:圆心为原点O,设PS与PO的夹角为a,则|
|=|
|=
,
故
•
=|
||
|cos2α=
cos2α=
cos2α
=
cos2α,记cos2α=u,u∈[-1,1]
则
•
=
u=-
=-[(u-1)+
+3]=(1-u)+
-3
≥2
-3=2
-3,
故
•
的最小值为2
-3,
故选D
| PS |
| PT |
| 1 |
| tanα |
故
| PS |
| PT |
| PS |
| PT |
| 1 |
| tan2α |
| cos2α |
| sin2α |
=
| 1+cos2α |
| 1-cos2α |
则
| PS |
| PT |
| 1+u |
| 1-u |
| (u-1)2+3(u-1)+2 |
| u-1 |
=-[(u-1)+
| 2 |
| u-1 |
| 2 |
| 1-u |
≥2
(1-u)
|
| 2 |
故
| PS |
| PT |
| 2 |
故选D
点评:本题考查圆切线的性质、三角函数的二倍角公式、向量的数量积公式、基本不等式求函数的最值,属于中档题.

练习册系列答案
相关题目
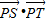 的最小值为( )
的最小值为( )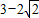
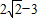

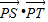 的最小值为( )
的最小值为( )