题目内容
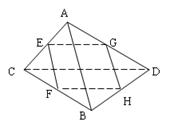
如图：线段AB、CD所在的直线是异面直线，E、F、G、H分别是线段AC、CB、BD、DA的中点，P、Q两点分别是AB和CD上的任意点，求证：PQ被平面EFGH平分、
证明见解析
解析:
证明：PQ∩平面EEFGH=N，
连PC，设PC∩EF=M
平面PCQ∩平面EFGH=MN，
CQ∥平面EFGH
∴MN∥CQ
因为EF是△ABC的中位线，所以M是CP的中点，则N是PQ的中点，
即 PQ被平面EFGH平分
练习册系列答案
相关题目
解析:
题目内容
如图：线段AB、CD所在的直线是异面直线，E、F、G、H分别是线段AC、CB、BD、DA的中点，P、Q两点分别是AB和CD上的任意点，求证：PQ被平面EFGH平分、
证明见解析
证明：PQ∩平面EEFGH=N，
连PC，设PC∩EF=M
平面PCQ∩平面EFGH=MN，
CQ∥平面EFGH
∴MN∥CQ
因为EF是△ABC的中位线，所以M是CP的中点，则N是PQ的中点，
即 PQ被平面EFGH平分
可以表示为( )．
