题目内容
设 若
若 的最小值为( )
的最小值为( )
| A. 8 | B. 4 | C.1 | D.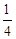 |
B
解析试题分析:本题显然要先求出 之间满足的关系,
之间满足的关系, 是
是 与
与 的等比中项,得
的等比中项,得 ,即
,即 ,∴
,∴ .由基本不等式得
.由基本不等式得 ,即
,即 ,
, 时取等号. ∴
时取等号. ∴ .选B.
.选B.
考点:基本不等式.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
设第一象限内的点 满足约束条件
满足约束条件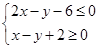 ,若目标函数
,若目标函数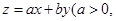
 的最大值为40,则
的最大值为40,则 的最小值为( )
的最小值为( )
A. | B. | C.1 | D.4 |
已知关于x的不等式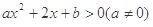 的解集是
的解集是 ,且a>b,则
,且a>b,则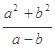 的最小值是( )
的最小值是( )
A.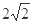 | B.2 | C.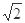 | D.1 |
若 和
和 均为非零实数,则下列不等式中恒成立的是( )
均为非零实数,则下列不等式中恒成立的是( )
A. . . | B.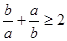 . . |
C.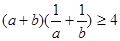 . . | D.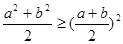 . . |
函数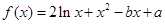
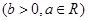 在点
在点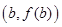 处的切线斜率的最小值是( )
处的切线斜率的最小值是( )
A.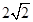 | B.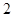 | C.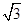 | D. |
若正数 满足
满足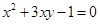 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C.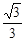 | D. |
函数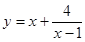
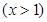 的最小值是( )
的最小值是( )
| A.3 | B.4 | C.5 | D.6 |
“a>b>0”是“ab< ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知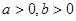 ,且函数
,且函数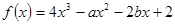 在
在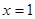 处有极值,则
处有极值,则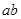 的最大值等于( )
的最大值等于( )
A. | B.3 | C.6 | D.9 |