题目内容
函数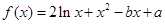
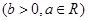 在点
在点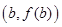 处的切线斜率的最小值是( )
处的切线斜率的最小值是( )
A.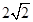 | B.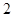 | C.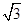 | D. |
A
解析试题分析:∵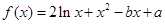 ,∴
,∴ ,
,
∴ ,当且仅当
,当且仅当 时取等号,∴
时取等号,∴ 的最小值为
的最小值为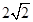 .
.
考点:1.利用导数求切线的斜率;2.基本不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设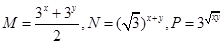 (
(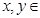 R
R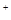 ,且
,且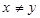 ), 则
), 则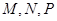 大小关系为( )
大小关系为( )
A.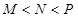 | B.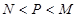 | C. | D. |
函数y=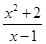 (x>1)的最小值是( )
(x>1)的最小值是( )
A.2 +2 +2 | B.2 -2 -2 | C.2 | D.2 |
下列函数中,最小值为4的是 ( )
A. | B. |
C. | D.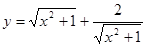 |
设 若
若 的最小值为( )
的最小值为( )
| A. 8 | B. 4 | C.1 | D.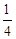 |
若 ,则
,则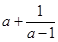 的最小值是( )
的最小值是( )
A.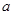 | B.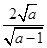 | C.2 | D.3 |
已知 是关于
是关于 的一元二次方程
的一元二次方程 的两根,若
的两根,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 ,若存在正实数
,若存在正实数 ,使得方程
,使得方程 在区间(2,+
在区间(2,+ )上有两个根
)上有两个根 ,其中
,其中 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
设正实数x,y,z满足x2-3xy+4y2-z=0,则当 取得最小值时,x+2y-z的最大值为( )
取得最小值时,x+2y-z的最大值为( )
| A.0 | B. |
| C.2 | D. |