Question

（09年海淀区二模文）（14分）

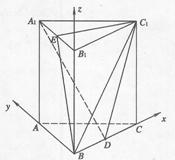
如图，直三棱柱A₁B₁C₁―ABC中，D、E分别是BC、A₁B₁的中点.

   （1）证明：BE//平面A₁DC₁；

   （2）求AB=BC=AA₁=1，∠ABC=90°求二面角B₁―BC_­1―E的正切值.

Answer 1

解析：方法1：（I）证明：取A₁C₁的中点F，

       连结EF，DF  …………………1分

       E中A₁B₁的中点

      

       又四边形BCC₁B₁是矩形，

      

D是BC的中点，

      

四边形EFDB是平行四边形，

          4分

     6分

   （II）连结B₁C交BC₁于O点，连结EO ……..  7分

      

       即

       又

       平面BC₁B₁    9分

      

       ，且四边形BCB₁C₁是正方形，

           10分

   

       在平面BC₁B₁上的射影，

      

       是二面角B₁―BC₁―E的平面角，   11分

       在直角

      

           13分

          14分

       方法2：

   （I）证明同方法1    6分

   （II）以B为坐标原点建立空间直角坐标系

      

       可得   7分

       则   8分

       设平面BEC₁的法向量为

       由

       可得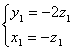    9分

       令   10分

       又由平面B₁BC₁，

       则平面的法向量

          12分

   （注：公式、结果各一分）

       由图可知二面角B₁―BC₁―E小于90°

       所以二面角的大小为.                                               13分

       ∴二面角的正切值为                14分