题目内容
13．集合A={x∈N|x≤4}，B={x|x2-4＜0}，则A∩B=（ ）| A． | {x|0≤x＜2} | B． | {x|-2＜x＜2} | C． | {0，1} | D． | {-2，0，1，2} |
分析 先化简集合A，B，再根据交集的运算即可．
解答 解：集合A={x∈N|x≤4}={0，1，2，3，4}，
由集合B中的不等式x2-4＜0，
因式分解得：（x+2）（x-2）＜0，
解得：-2＜x＜2，
所以集合B=（-2，2）；
则集合A∩B={0，1}．
故选：C．
点评 此题属于以不等式解集中的奇数解为平台，考查了交集的运算，是一道基础题．也是高考中常考的题型．
练习册系列答案
阅读快车系列答案
相关题目
3．
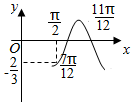已知函数f（x）=Acos（ωx+φ）的图象如图所示，则f（$\frac{5π}{6}$）=（ ）
已知函数f（x）=Acos（ωx+φ）的图象如图所示，则f（$\frac{5π}{6}$）=（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
4．设α，β是两个不同的平面，l，m是两条不同的直线，α∩β=m，记α1为直线l与平面α所成的角，A={l|l?β}，B={α1|l∈A}，若对任意α1∈B，存在α${\;}_{{l}_{0}}$∈B，恒有α1＜α${\;}_{{l}_{0}}$，则（ ）
| A． | α⊥β | B． | α与β不垂直 | C． | l0⊥a | D． | l0⊥m |
1．复数z=$\frac{（2i-3）（i-2）}{i}$的实部和虚部之和为（ ）
| A． | -3 | B． | 4 | C． | 3 | D． | -11 |
8．焦点为（6，0）且与双曲线$\frac{x^2}{2}$-y2=1有相同渐近线的双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1 | B． | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 | C． | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D． | $\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1 |
3．己知a，b∈R，下列命题正确的是（ ）
| A． | 若a＞b，则$\frac{1}{a}$＞$\frac{1}{b}$ | B． | 若a＞b，则$\frac{1}{a}$＜$\frac{1}{b}$ | C． | 若|a|＞b，则a2＞b2 | D． | 若a＞|b|，则a2＞b2 |