题目内容
设函数h(x)=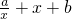 ,对任意
,对任意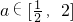 ,都有h(x)≤10在
,都有h(x)≤10在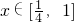 恒成立,则实数b的取值范围是________.
恒成立,则实数b的取值范围是________.
b≤10-
分析:由题意,求出函数h(x)=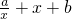 的最小值即可,由于
的最小值即可,由于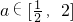 ,故需要进行分类讨论.
,故需要进行分类讨论.
解答:由题意,求出函数h(x)=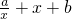 的最小值即可
的最小值即可
当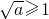 ,即a∈[1,2]时,函数在
,即a∈[1,2]时,函数在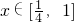 上单调减,所以x=1时,函数取得最小值为a+b+1
上单调减,所以x=1时,函数取得最小值为a+b+1
∴a+b+1≤10在a∈[1,2]时,恒成立
∴b≤9-a,∴b≤7
当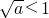 ,即
,即 )时,函数在
)时,函数在 上单调减,在
上单调减,在 上单调增,所以x=
上单调增,所以x= 时,函数取得最小值为
时,函数取得最小值为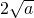 +b
+b
∴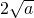 +b≤10在
+b≤10在 )时,恒成立
)时,恒成立
∴b≤10-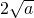 ,∴b≤10-
,∴b≤10-
综上知,b≤10-
故答案为:b≤10-
点评:本题考查恒成立问题,考查函数的最值,考查函数的单调性,考查分类讨论的数学思想,属于中档题.

分析:由题意,求出函数h(x)=
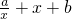 的最小值即可,由于
的最小值即可,由于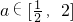 ,故需要进行分类讨论.
,故需要进行分类讨论.解答:由题意,求出函数h(x)=
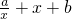 的最小值即可
的最小值即可当
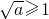 ,即a∈[1,2]时,函数在
,即a∈[1,2]时,函数在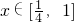 上单调减,所以x=1时,函数取得最小值为a+b+1
上单调减,所以x=1时,函数取得最小值为a+b+1∴a+b+1≤10在a∈[1,2]时,恒成立
∴b≤9-a,∴b≤7
当
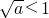 ,即
,即 )时,函数在
)时,函数在 上单调减,在
上单调减,在 上单调增,所以x=
上单调增,所以x= 时,函数取得最小值为
时,函数取得最小值为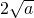 +b
+b∴
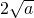 +b≤10在
+b≤10在 )时,恒成立
)时,恒成立∴b≤10-
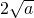 ,∴b≤10-
,∴b≤10-
综上知,b≤10-

故答案为:b≤10-

点评:本题考查恒成立问题,考查函数的最值,考查函数的单调性,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目