题目内容
时维壬辰,序属仲春,值春耕播种时机,某中学生物研究性学习小组对春季昼夜温差大小与水稻发芽率之间的关系进行研究,记录了实验室4月10日至4月14日的每天昼夜温差与每天每50颗稻籽浸泡后的发芽数,得到如下资料:
(Ⅰ)从4月10日至4月14日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于14”的概率;
(Ⅱ)根据表中的数据可知发芽数y(颗)与温差x(oC)呈线性相关,请求出发芽数y关于温差x的线性回归方程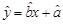 .
.
(参考公式:回归直线方程式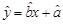 ,其中
,其中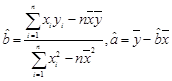 )
)
| 日 期 | 4月10日 | 4月11日 | 4月12日 | 4月13日 | 4月14日 |
| 温 差x(oC) | 10 | 12 | 13 | 14 | 11 |
| 发芽数y(颗) | 11 | 13 | 14 | 16 | 12 |
(Ⅱ)根据表中的数据可知发芽数y(颗)与温差x(oC)呈线性相关,请求出发芽数y关于温差x的线性回归方程
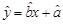 .
.(参考公式:回归直线方程式
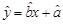 ,其中
,其中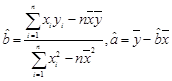 )
)(1) (2)
(2)
 (2)
(2)
(I)本题属于古典概型,先求出构成基本事件(m,n)有10个.其中“m,n均小于14”的有3个,其概率为 .
.
(II)先求 ,然后利用
,然后利用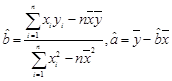 ,求出
,求出 和
和 代入
代入 .
.
解:(Ⅰ)m,n构成的基本事件(m,n)有:(11,13),(11,14),(11,16),(11,12),(13,14),(13,16),(13,12),(14,16),(14,12),(16,12),共有10个.
其中“m,n均小于14”的有3个,其概率为 . ..........6分
. ..........6分
(Ⅱ)∵
∴ .
.
于是, .
.
故所求线性回归方程为 ...........12分
...........12分
 .
.(II)先求
 ,然后利用
,然后利用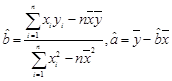 ,求出
,求出 和
和 代入
代入 .
.解:(Ⅰ)m,n构成的基本事件(m,n)有:(11,13),(11,14),(11,16),(11,12),(13,14),(13,16),(13,12),(14,16),(14,12),(16,12),共有10个.
其中“m,n均小于14”的有3个,其概率为
 . ..........6分
. ..........6分 (Ⅱ)∵

∴
 .
. 于是,
 .
. 故所求线性回归方程为
 ...........12分
...........12分 
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目


 ,则
,则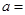 ( )
( )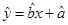 ,下列说法中不正确的是( )
,下列说法中不正确的是( )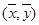
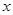 增加一个单位时,
增加一个单位时,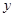 平均增加
平均增加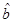 个单位
个单位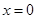 时,可能有
时,可能有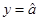
 ,则
,则 ___________.
___________.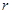 ;
; 必经过( )
必经过( )



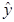 =bx+a中的b≈0.7,试预测加工10个零件需小时数为( )。(已知
=bx+a中的b≈0.7,试预测加工10个零件需小时数为( )。(已知 )
)