题目内容
已知a,b,c分别为△ABC三个内角A,B,C的对边,c=
asinC-ccosA
(1)求角A;
(2)若a=2,△ABC的面积为
,求b,c.
| 3 |
(1)求角A;
(2)若a=2,△ABC的面积为
| 3 |
(1)由正弦定理
=
=
化简已知的等式得:sinC=
sinAsinC-sinCcosA,
∵C为三角形的内角,∴sinC≠0,
∴
sinA-cosA=1,
整理得:2sin(A-
)=1,即sin(A-
)=
,
∴A-
=
或A-
=
,
解得:A=
或A=π(舍去),
则A=
;
(2)∵a=2,sinA=
,cosA=
,△ABC的面积为
,
∴
bcsinA=
bc=
,即bc=4①;
∴由余弦定理a2=b2+c2-2bccosA得:4=b2+c2-bc=(b+c)2-3bc=(b+c)2-12,
整理得:b+c=4②,
联立①②解得:b=c=2.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| 3 |
∵C为三角形的内角,∴sinC≠0,
∴
| 3 |
整理得:2sin(A-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴A-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
解得:A=
| π |
| 3 |
则A=
| π |
| 3 |
(2)∵a=2,sinA=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴
| 1 |
| 2 |
| ||
| 4 |
| 3 |
∴由余弦定理a2=b2+c2-2bccosA得:4=b2+c2-bc=(b+c)2-3bc=(b+c)2-12,
整理得:b+c=4②,
联立①②解得:b=c=2.

练习册系列答案
相关题目
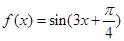 .
.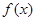 的单调递增区间;
的单调递增区间;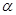 是第二象限角,
是第二象限角,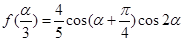 ,求
,求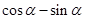 的值.
的值.