题目内容
如图所示,四边形ABCD为矩形,点M是BC的中点,CN=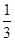 CA,用向量法证明:
CA,用向量法证明:
(1)D、N、M三点共线;(2)若四边形ABCD为正方形,则DN=BN. K^S*5U.C ^S*5U.C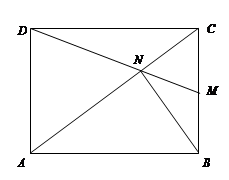

(1)设
∵
 ………3分
………3分
∴ ,且DM与DN有公共点D
,且DM与DN有公共点D
∴D、N、M三点共线
(2)若四边形ABCD为正方形,则 且
且
∵
∴
同理可得 ∴
∴ ,即DN=BN
,即DN=BN
备注:利用坐标来运算的相应得分.
解析

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
在极坐标系中与圆 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A. | B. |
C. | D. |
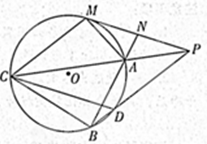
 外有一点
外有一点 ,作圆
,作圆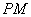 ,
,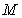 为切点,过
为切点,过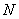 ,作割线
,作割线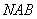 ,交圆于
,交圆于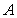 、
、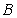 两点,连接
两点,连接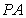 并延长,交圆
并延长,交圆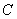 ,连续
,连续 交圆
交圆 ,若
,若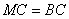 .
.
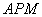 ∽△
∽△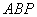 ;
;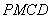 是平行四边形.
是平行四边形.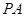 与圆
与圆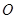 相切于点
相切于点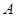 ,经过点
,经过点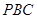 交圆
交圆 、
、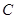 ,
,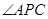 的平分线分别交
的平分线分别交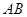 、
、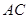 于点
于点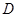 、
、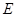 .
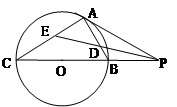
.
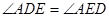 .
.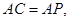 求
求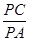 的值.
的值. 中,∠
中,∠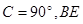 是角平分线,
是角平分线, 交
交 于
于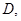 ⊙
⊙ 是△
是△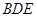 的外接圆。
的外接圆。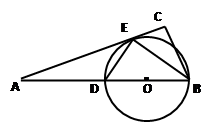
 是⊙
是⊙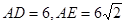 ,求
,求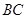 的长。
的长。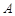 ,D为
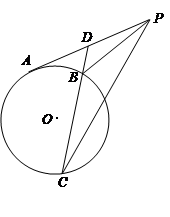
,D为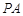 的中点,过点D引割线交⊙O于
的中点,过点D引割线交⊙O于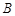 、
、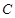 两点.
两点.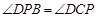 .
.
 中,
中, ,
, 平分
平分 交
交 于点
于点 ,点
,点 在
在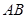 上,
上, .
.
 的外接圆的切线;
的外接圆的切线; ,求
,求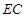 的长.
的长. 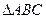 中,
中,
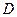 在线
在线 段
段 上,且
上,且 ,
,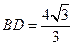
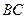 的长;
的长; 的面积.
的面积.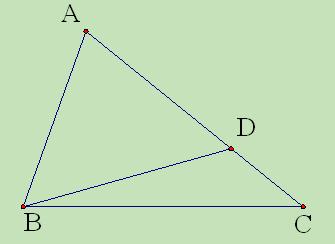
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 内接于
内接于 ,
, ,过
,过 点的切线交
点的切线交 的延长线于
的延长线于 点。求证:
点。求证: 。
。