题目内容
在极坐标系中与圆 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A. | B. |
C. | D. |
A
解析试题分析:根据 ,可将极坐标方程转化为直角坐标方程进行判断,
,可将极坐标方程转化为直角坐标方程进行判断, 变形后可得
变形后可得 ,即
,即 ,化为标准方程
,化为标准方程 ,对于A:
,对于A: ,即x=2,显然相切;对于B:
,即x=2,显然相切;对于B: ,即y=2,不相切;而C,D表示的都是圆的方程,不符,∴选A
,即y=2,不相切;而C,D表示的都是圆的方程,不符,∴选A
考点:1、直线与圆的位置关系;2、极坐标与直角坐标的互化.

练习册系列答案
相关题目
直线 被圆
被圆 截得的弦长为( )
截得的弦长为( )
A. | B. | C. | D. |
若直线的参数方程为 ,则直线的斜率为( ).
,则直线的斜率为( ).
A. | B.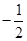 | C. | D. |
直线 被圆
被圆 截得的弦长为( )
截得的弦长为( )
A. | B. | C. | D. |
 是曲线
是曲线 上任意一点,则
上任意一点,则 的最大值是 ( )
的最大值是 ( )
| A.36 | B.6 | C.26 | D.25 |
椭圆 
 是参数
是参数 的离心率是
的离心率是
A. | B. | C. | D. |
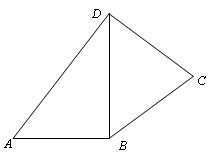
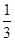 CA,用向量法证明:
CA,用向量法证明: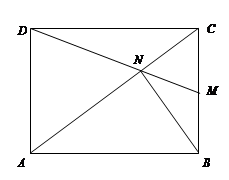

 为极点、
为极点、 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点 的极坐标为
的极坐标为 ,曲线
,曲线 的参数方程为
的参数方程为 (
(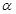 为参数),则点
为参数),则点 BD,
BD, 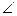 ABD=
ABD=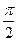 ,设
,设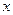 ,四边形ABCD的面积为S,求函数S=
,四边形ABCD的面积为S,求函数S=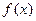 的最大值.
的最大值.