Question

【题目】如图，F1 ， F2分别是椭圆C： =1（a＞b＞0）的左、右焦点，且焦距为2 ，动弦AB平行于x轴，且|F1A|+|F1B|=4．

（1）求椭圆C的方程；
（2）若点P是椭圆C上异于点 、A，B的任意一点，且直线PA、PB分别与y轴交于点M、N，若MF2、NF2的斜率分别为k1、k2 ， 求证：k1k2是定值．

Answer 1

【答案】
（1）

解：∵焦距2 ，∴2c=2 ，得c= ，

由椭圆的对称性及已知得|F1A|=|F2B|，又∵|F1A|+|F1B|=4，|F1B|+|F2B|=4，

因此2a=4，a=2，于是b= ，因此椭圆方程为

（2）

解：设B（x0，y0），P（x1，y1），则A（﹣x0，y0），

直线PA的方程为 ，令x=0，得 ，

故M（0， ）；

直线PB的方程为 ，令x=0，得 ，

故N（0， ）；

∴ ， ，

因此 ．

∵A，B在椭圆C上，∴ ，

∴

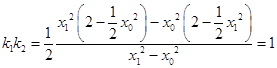
【解析】（1）由题意焦距求得c，由对称性结合|F1A|+|F1B|=4可得2a，再由隐含条件求得b，则椭圆方程可求；（2）设B（x0 ， y0），P（x1 ， y1），则A（﹣x0 ， y0），分别写出PA、PB所在直线方程，求出M、N的坐标，进一步求出MF2、NF2的斜率分别为k1、k2 ， 结合A、B在椭圆上可得k1k2是定值．