题目内容
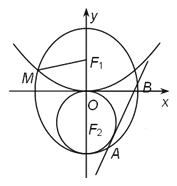
【题目】已知
分别为椭圆
的上、下焦点， 
是抛物线
的焦点，点
是
与
在第二象限的交点，且
．
（1）求椭圆
的方程；
（2）与圆
相切的直线
交椭圆
于
，
若椭圆
上一点
满足
，求实数
的取值范围．
【答案】(1) 
(2) 
【解析】试题分析：（1）由题意知
，所以
，又由抛物线定义可知
，得
，于是易知
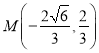，从而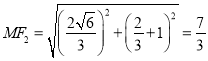
，由椭圆定义知， 
，得
，故
，从而椭圆的方程为
；（2）设
，则由
知， 
， 
，且
①，又直线
与圆
相切，所以有
，由
，可得
②，又联立
，消去
得
，且
恒成立，且
， 
，所以
，所以得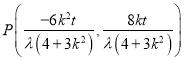
，代入①，结合②得： 
， 
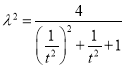，利用二次函数求分母取值范围
，所以
，即
的取值范围为
．
试题解析：（1）由题意
，所以
，又由抛物线定义可知
，得
，
于是易知
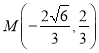，从而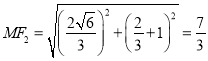
，
由椭圆定义知， 
，得
，故
，
从而椭圆的方程为
．
（2）设
，则由
知，
， 
，且
①
又直线
与圆
相切，所以有
，
由
，可得
②
又联立
，消去
得
且
恒成立，且
， 
，
所以
，所以得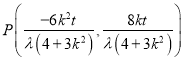
，
代入①式得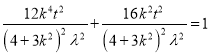
，所以
，
又将②式代入得，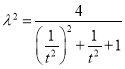 
， 
，
易知
，且
，所以
，
所以
的取值范围为
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在下图中的两条线段上，该股票在30天内（包括30天）的日交易量Q（万股）与时间t（天）的部分数据如下表所示．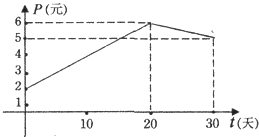 
第t天 | 4 | 10 | 16 | 22 |
Q（万股） | 36 | 30 | 24 | 18 |
（1）根据提供的图象，写出该种股票每股交易价格P（元）与时间t（天）所满足的函数关系式；
（2）根据表中数据确定日交易量Q（万股）与时间t（天）的一次函数关系式；
（3）在（2）的结论下，用y（万元）表示该股票日交易额，写出y关于t的函数关系式，并求出这30天中第几日交易额最大，最大值为多少？
