题目内容
设函数f（x）=sinx+x2013，令f1（x）=f′（x），是f2（x）=f1′（x），…，fn+1（x）=fn′（x）（n∈N+），则f2013=
cosx+2013!
cosx+2013!
．分析：分别求出函数的导数，通过观察每个式子的特点寻找出规律，根据归纳推理得到结果．
解答：解：由题意可知：f1(x)=f′(x)=cos?x+2013?x2012，
f2(x)=f1′(x)=-sin?x+2013?2012x2011，
f3(x)=f2′(x)=-cos?x+2013?2012?2011x2010，
f4(x)=f3′(x)=sin?x+2013?2012?2011?2010x2009，
f5(x)=f4′(x)=cos?x+2013?2012?2011?2010?2009x2008，
所以根据归纳推理可知，
f2013（x）=f2012'（x）=cos?x+2013?2012???1=cos?x+2013!，
故答案为：cosx+2013!．
f2(x)=f1′(x)=-sin?x+2013?2012x2011，
f3(x)=f2′(x)=-cos?x+2013?2012?2011x2010，
f4(x)=f3′(x)=sin?x+2013?2012?2011?2010x2009，
f5(x)=f4′(x)=cos?x+2013?2012?2011?2010?2009x2008，
所以根据归纳推理可知，
f2013（x）=f2012'（x）=cos?x+2013?2012???1=cos?x+2013!，
故答案为：cosx+2013!．
点评：本题主要考查导数的运算以及归纳推理的应用，考查学生的运算能力，综合性较强．
练习册系列答案
一线名师权威作业本系列答案
相关题目
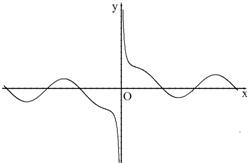如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g （ x ）=| 1 |
| x |
A、
| ||
| B、f（x）g（x） | ||
| C、f（x）-g（x） | ||
| D、f（x）+g（x） |
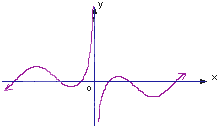设函数f（x）=sinx，g（x）=