题目内容
已知函数 =
= ,
, =
= ,若曲线
,若曲线 和曲线
和曲线 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线
(Ⅰ)求 ,
, ,
, ,
, 的值;
的值;
(Ⅱ)若 ≥-2时,
≥-2时, ≤
≤ ,求
,求 的取值范围.
的取值范围.
(Ⅰ)由已知得 ,
,
而 =
= ,
, =
= ,∴
,∴ =4,
=4, =2,
=2, =2,
=2, =2;
=2;
(Ⅱ)由(Ⅰ)知, ,
, ,
,
设函数 =
= =
= (
( ),
),
 =
= =
= ,
,
有题设可得 ≥0,即
≥0,即 ,
,
令 =0得,
=0得,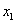 =
= ,
, =-2,
=-2,
(1)若 ,则-2<
,则-2<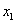 ≤0,∴当
≤0,∴当 时,
时, <0,当
<0,当 时,
时, >0,即
>0,即 在
在 单调递减,在
单调递减,在 单调递增,故
单调递增,故 在
在 =
=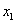 取最小值
取最小值 ,而
,而 =
= =
= ≥0,
≥0,
∴当 ≥-2时,
≥-2时, ≥0,即
≥0,即 ≤
≤ 恒成立,
恒成立,
(2)若 ,则
,则 =
= ,
,
∴当 ≥-2时,
≥-2时, ≥0,∴
≥0,∴ 在(-2,+∞)单调递增,而
在(-2,+∞)单调递增,而 =0,
=0,
∴当 ≥-2时,
≥-2时, ≥0,即
≥0,即 ≤
≤ 恒成立,
恒成立,
(3)若 ,则
,则 =
= =
= <0,
<0,
∴当 ≥-2时,
≥-2时, ≤
≤ 不可能恒成立,
不可能恒成立,
综上所述, 的取值范围为[1,
的取值范围为[1, ].
].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
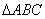 中,角A、B、C的对边分别为a、b、c,且
中,角A、B、C的对边分别为a、b、c,且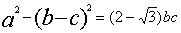 ,
, ,
,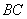 边上的中线
边上的中线 的长为
的长为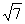 。
。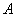 和角
和角 的大小;
的大小; 是函数
是函数 的图像如图所示,则
的图像如图所示,则 的图像最有可能的是( ).
的图像最有可能的是( ). 




 与直线
与直线 围成的封闭图形的面积?
围成的封闭图形的面积? 个同类产品中(其中
个同类产品中(其中 个正品,
个正品, 个次品),任意抽取
个次品),任意抽取 个,下列事件是必然事件的是( )
个,下列事件是必然事件的是( ) .
. .
. .至少有一个正品
.至少有一个正品  .至少有一个次品
.至少有一个次品 +
+ +
+ =
= ,则△PAB的面积与△ABC的面积比为( )
,则△PAB的面积与△ABC的面积比为( ) 2:3
2:3  1:3
1:3  1:4
1:4  1:6
1:6 于F(不与B重合),直线
于F(不与B重合),直线 与
与 ;(2)
;(2) .
.