题目内容
投掷一枚质地均匀的骰子两次,若第一次面向上的点数小于第二次面向上的点数我们称其为前效实验,若第二次面向上的点数小于第一次面向上的点数我们称其为后效实验,若两次面向上的点数相等我们称其为等效试验.那么一个人投掷该骰子两次后出现等效实验的概率是( )
A. | B.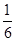 | C. | D. |
B
解析试题分析:投掷一枚质地均匀的骰子两次,其所有的可能性为:


 。共36种。
。共36种。
其中两次面向上的点数相等的有 ,共6中,
,共6中,
所以一个人投掷该骰子两次后出现等效实验的概率是 。
。
考点:古典概型;随机事件的概率。
点评:当基本事件的个数不是太多时,我们可以一一列举,但要注意,列举时要不重不漏。

练习册系列答案
相关题目
从甲口袋摸出一个红球的概率是 ,从乙口袋中摸出一个红球的概率是
,从乙口袋中摸出一个红球的概率是 ,则
,则 是( )
是( )
| A.2个球不都是红球的概率 | B.2个球都是红球的概率 |
| C.至少有一个红球的概率 | D.2个球中恰好有1个红球的概率 |
从1,2,3,4四个数字中任取两个数求和,则和恰为偶数的概率是( )
A. | B. | C. | D. |
若以连续掷两次骰子分别得到的点数 作为点
作为点 的坐标,则点
的坐标,则点 落在圆
落在圆 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
如图,某人向圆内投镖,如果他每次都投入圆内,那么他投中正方形区域的概率为
A. | B. | C. | D. |
 ,则“出现1点或2点”的概率为( ).
,则“出现1点或2点”的概率为( ).
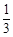



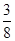


 内的任意位置,如果通过大量的实验发现粒子落入△
内的任意位置,如果通过大量的实验发现粒子落入△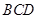 内的频率稳定在
内的频率稳定在 附近,那么点
附近,那么点 和点
和点 到时直线
到时直线 的距离之比约为( )
的距离之比约为( )






