题目内容
设F是抛物线G:x2=4y的焦点,点P是F关于原点的对称点.
(Ⅰ)过点P作抛物线G的切线,若切点在第一象限,求切线方程;
(Ⅱ)试探究(Ⅰ)中的抛物线G的切线与动圆x2+(y-m)2=5,m∈R的位置关系.
(Ⅰ)过点P作抛物线G的切线,若切点在第一象限,求切线方程;
(Ⅱ)试探究(Ⅰ)中的抛物线G的切线与动圆x2+(y-m)2=5,m∈R的位置关系.
分析:( I)利用导数求切线的斜率,假设切线方程,利用切点在切线上,即可求得切线方程;
(Ⅱ)探求圆心到切线的距离与圆的半径的关系,从而确定(Ⅰ)中的抛物线G的切线与动圆x2+(y-m)2=5,m∈R的位置关系.
(Ⅱ)探求圆心到切线的距离与圆的半径的关系,从而确定(Ⅰ)中的抛物线G的切线与动圆x2+(y-m)2=5,m∈R的位置关系.
解答:解:( I)设切点Q(x0,
)(x0>0).
由y′=
,知抛物线在Q点处的切线斜率为
,故所求切线方程y-
=
(x-x0). (2分)
即y=
x-
. (4分)
∵抛物线x2=4y的焦点为F(0,1),点P是F关于原点的对称点
∴P(0,-1)
因为点P(0,-1)在切线上.
所以-1=-
,
∴
=4,
∵x0>0
∴x0=2. (6分)
∴所求切线方程为y=x-1. (7分)
(Ⅱ) x2+(y-m)2=5,m∈R半径为r=
,圆心(0,m)到直线x-y-1=0的距离d=
=
若d>r,
>
,m>
-1或m<-
-1时,x-y-1=0与圆相离,(9分)
若d=r,
=
,m=
-1或m=-
-1时,x-y-1=0与圆相切,(11分)
若d<r,
<
,-
-1<m=
-1时,x-y-1=0与圆相交,(13分)
综上,若m>
-1或m<-
-1时(Ⅰ)中抛物线G的切线与动圆x2+(y-m)2=5相离,
若m=
-1或m=-
-1时(Ⅰ)中的抛物线G的切线与动圆x2+(y-m)2=5相切,
若-
-1<m=
-1时(Ⅰ)中的抛物线G的切线与动圆x2+(y-m)2=5相交 (14分)
| ||
| 4 |
由y′=
| x |
| 2 |
| x0 |
| 2 |
| ||
| 4 |
| x0 |
| 2 |
即y=
| x0 |
| 2 |
| ||
| 4 |
∵抛物线x2=4y的焦点为F(0,1),点P是F关于原点的对称点
∴P(0,-1)
因为点P(0,-1)在切线上.
所以-1=-
| ||
| 4 |
∴
| x | 2 0 |
∵x0>0
∴x0=2. (6分)
∴所求切线方程为y=x-1. (7分)
(Ⅱ) x2+(y-m)2=5,m∈R半径为r=
| 5 |
| |-m-1| | ||
|
| |m+1| | ||
|
若d>r,
| |m+1| | ||
|
| 5 |
| 10 |
| 10 |
若d=r,
| |m+1| | ||
|
| 5 |
| 10 |
| 10 |
若d<r,
| |m+1| | ||
|
| 5 |
| 10 |
| 10 |
综上,若m>
| 10 |
| 10 |
若m=
| 10 |
| 10 |
若-
| 10 |
| 10 |
点评:本题重点考查抛物线的切线,考查直线与圆的位置关系,解题时运用导数为工具,利用圆心到直线的距离与半径的关系,研究直线与圆的位置关系.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
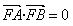 ,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。
,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。