题目内容
设F是抛物线G:x2=4y的焦点。
(1)过点P(0,-4)作抛物线G的切线,求切线方程;
(2)设A,B为抛物线G上异于原点的两点,且满足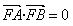 ,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。
,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。
(1)过点P(0,-4)作抛物线G的切线,求切线方程;
(2)设A,B为抛物线G上异于原点的两点,且满足
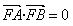 ,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。
,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。解:(1)设切点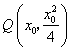
由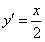 ,知抛物线在Q点处的切线斜率为
,知抛物线在Q点处的切线斜率为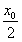 ,
,
故所求切线方程为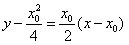
即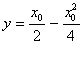
因为点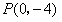 在切线上
在切线上
所以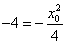 ,
,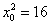 ,
,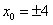
所求切线方程为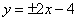 。
。
(2)设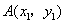 ,
,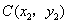
由题意知,直线AC的斜率k存在,由对称性,不妨设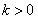
因直线AC过焦点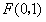 ,
,
所以直线AC的方程为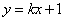
点 的坐标满足方程组
的坐标满足方程组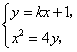
得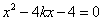 ,
,
由根与系数的关系知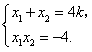
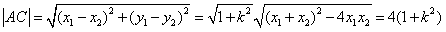
因为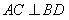 ,
,
所以BD的斜率为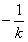 ,
,
从而BD的方程为
同理可求得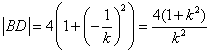
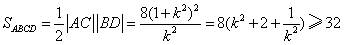
当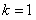 时,等号成立
时,等号成立
所以,四边形面积的最小值为32。
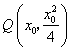
由
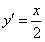 ,知抛物线在Q点处的切线斜率为
,知抛物线在Q点处的切线斜率为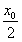 ,
,故所求切线方程为
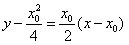
即
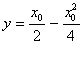
因为点
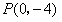 在切线上
在切线上所以
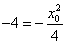 ,
,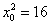 ,
,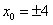
所求切线方程为
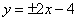 。
。(2)设
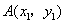 ,
,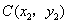
由题意知,直线AC的斜率k存在,由对称性,不妨设
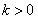
因直线AC过焦点
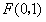 ,
,所以直线AC的方程为
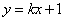
点
 的坐标满足方程组
的坐标满足方程组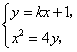
得
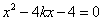 ,
,由根与系数的关系知
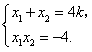
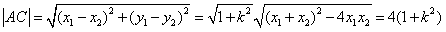
因为
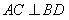 ,
,所以BD的斜率为
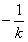 ,
,从而BD的方程为

同理可求得
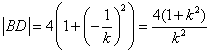
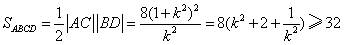
当
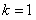 时,等号成立
时,等号成立所以,四边形面积的最小值为32。

练习册系列答案
相关题目